تکانه زاویه‌ای

این ژیروسکوپ به علت بقای تکانهٔ زاویه‌ای سرپا می‌ماند

در فیزیک، تکانهٔ زاویه‌ای یا تکانهٔ دورانی (به انگلیسی Angular momentum) (در فارسی به آن گشتاور دورانی یا گشتاور زاویه‌ای نیز گفته می‌شود) کمیتی برداری است که برای بیان وضعیت حرکتی سیستم‌های در حال حرکت دورانی مورد استفاده قرار می‌گیرد. با این که سرعت زاویه‌ای مرسوم‌ترین کمیت برای بیان وضعیت حرکتی جسم در حال دوران است، اما تکانهٔ زاویه‌ای نسبت به آن اطلاعات بیشتری را دربردارد. تکانهٔ زاویه‌ای یک سیستم به سرعت زاویه‌ای، جرم و نحوهٔ توزیع جرم سیستم حول محور دوران یا مرکز دوران وابسته است. تکانهٔ زاویه‌ای همواره نسبت به یک چارچوب مرجع سنجیده می‌شود.

تکانهٔ زاویه‌ای در مکانیک کلاسیک

تکانهٔ زاویه‌ای ذرهٔ در حال دوران حول یک محور

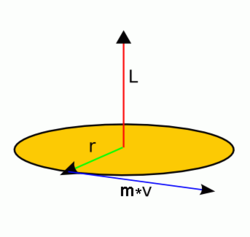
تکانهٔ زاویه‌ای یک ذره

تکانهٔ زاویه‌ای یک ذره به صورت ضرب خارجی بردارهای $𝐫$ (بردار مکان ذره نسبت به نقطهٔ مرجع) و تکانهٔ خطی $𝐩=m𝐯$ تعریف می‌شود:

$𝐋=𝐫\times 𝐩$

برای اجسام صلب رابطهٔ:

$L=I\times \omega$

هم، برقرار می‌باشد. الگو:پایان

وابستگی تکانهٔ زاویه‌ای به سرعت، جرم و توزیع جرم (موقعیت ذره نسبت به نقطهٔ مرجع) در رابطهٔ بالا مشهود است. بنا به تعریف، ضرب خارجی دو بردار شبه برداری است که بر هر دو بردار اصلی عمود است. پس، بردار تکانهٔ زاویه‌ای بر «صفحهٔ دوران ذره» عمود خواهد بود (شکل روبرو).

بنا به تعریف ضرب خارجی، تکانهٔ زاویه‌ای ذره را می‌توان به شکل زیر نیز نوشت: الگو:وسط‌چین

$𝐋=𝐫\times 𝐩=rmv\sin (\theta )$

الگو:پایان که در آن، $\theta$ زاویهٔ بین بردارهای مکان و سرعت است. با توجه به رابطهٔ بالا، یکای اندازه‌گیری تکانهٔ زاویه‌ای در دستگاه SI به صورت kg. m. m/s یا N. m. s یا j. sec خواهد بود.

تکانهٔ زاویه‌ای سامانه بس ذره‌ای

اگر سامانه شامل بیش از یک ذره باشد، تکانهٔ زاویه‌ای آن حول یک نقطه را می‌توان با جمع بستن تکانهٔ زاویه‌ای تک تک ذرات تشکیل دهندهٔ سامانه حول همان نقطه به دست آورد. به فرض آن که سامانه دارای $N$ ذره باشد، داریم:

$𝐋=\sum _{i=1}^N{𝐋}_i=\sum _{i=1}^N{𝐫}_i\times m_i{𝐯}_i$

که در آن، ${𝐫}_i$ مکان ذرهٔ $i$ام نسبت به نقطهٔ مرجع، $m_i$ جرم ذره و ${𝐯}_i$ سرعت آن است.

پایستگی تکانهٔ زاویه‌ای

در یک سامانه چرخشی، بنا بر قانون سوم حرکت تکانهٔ زاویه‌ای کل سامانه با گذشت زمان ثابت می‌ماند (حفظ می‌شود). نتیجهٔ پایستگی تکانهٔ زاویه‌ای همسانگردی در فضاست. همچنین با استفاده از قانون کنش و واکنش؛ قانون اول حرکت، نیز می‌توان گفت: " یک جسم صلب به حالت چرخش یکنواخت ادامه می‌دهد مگر اینکه اثر خارجی بر روی آن تأثیر کند، حرکت زاویه‌ای اصلی سامانه ثابت می‌ماند.

جستارهای وابسته

• تکانه
• ضرایب کلبش-گوردون
• بروریا کافمن

پیوند به بیرون

• پایستگی تکانه زاویه‌ای - یک فصل از یک کتاب تکست‌بوک برخط