چرپ

شکل موج چرپ خطی؛ یک موج سینوسی که در طول زمان به صورت خطی فرکانس افزایش می‌یابد

چِرپ الگو:به انگلیسی سیگنالی است که در آن، فرکانس با گذشت زمان افزایش می‌یابد (چرپ-بالارونده) یا کاهش می‌یابد (چرپ-پایین‌رونده). در برخی منابع، اصطلاح چرپ به جای سیگنال جاروب استفاده می‌شود. معمولاً برای سامانه‌های سونار، رادار، و لیزر و سایر کاربردها، مانند مخابرات طیف گسترده (به طیف گسترده چرپ مراجعه کنید) استفاده می‌شود. این نوع سیگنال از نظر بیولوژیکی الهام گرفته شده است و به عنوان یک پدیده به دلیل پراکندگی (وابستگی غیرخطی بین فرکانس و سرعت انتشار مولفه‌های موج) رخ می‌دهد. معمولاً با استفاده از یک فیلتر تطبیق‌شده، که می‌تواند بخشی از کانال انتشار باشد، جبران می‌شود. با این حال، بسته به معیار عملکرد خاص، فنون بهتری هم برای رادار و هم برای مخابرات وجود دارد. از آنجایی که در رادار و فضا مورد استفاده قرار گرفت، برای استانداردهای مخابراتی نیز مورد استفاده قرار گرفت. برای کاربردهای رادار خودرو، معمولاً شکل‌موج مدوله‌شده با فرکانس خطی (LFMW) نامیده می‌شود.

تعاریف

تعاریف پایه در اینجا به عنوان کمیت‌های فیزیک رایج، موقعیت (فاز)، سرعت (سرعت زاویه ای)، شتاب (چرپینگی) ترجمه می‌شوند. اگر شکل‌موج به صورت زیر تعریف شود: $$x(t)=\sin (\varphi (t))$$ سپس فرکانس زاویه‌ای لحظه‌ای، ω، به عنوان نرخ فازی که توسط مشتق اول فاز ارائه می‌شود، تعریف می‌شود، با فرکانس عادی لحظه‌ای، f، نسخه بهنجارشده آن است: $$\omega (t)=\frac{d\varphi (t)}{dt},f(t)=\frac{\omega (t)}{2\pi }$$در نهایت، چرپینگی زاویه‌ای لحظه‌ای الگو:به انگلیسی (نماد γ) به عنوان مشتق دوم فاز لحظه‌ای یا مشتق اول فرکانس زاویه‌ای لحظه‌ای تعریف می‌شود. $$\gamma (t)=\frac{d^2\varphi (t)}{d{t}^2}=\frac{d\omega (t)}{dt}$$ چرپینگی زاویه‌ای دارای واحدهای رادیان بر ثانیه (rad/s^۲) است؛ بنابراین، مشابه شتاب زاویه ای است.

چرپینگی عادی لحظه‌ای (نماد c) یک نسخه بهنجارشده است که به عنوان نرخ تغییر فرکانس لحظه‌ای تعریف می‌شود:$$c(t)=\frac{\gamma (t)}{2\pi }=\frac{df(t)}{dt}$$چرپینگی عادی دارای واحدهای مربع وارون ثانیه (s^−۲) است؛ بنابراین، مشابه شتاب دورانی است.

انواع

خطی

طیف‌نگارهٔ یک چیپ خطی. نمودار طیف‌نگار نرخ خطی تغییر فرکانس را به صورت تابعی از زمان نشان می‌دهد، در این مورد از ۰ تا ۷ کیلوهرتز، هر ۲٫۳ ثانیه تکرار می‌شود. شدت نمودار متناسب با محتوای انرژی در سیگنال در فرکانس و زمان مشخص شده است.

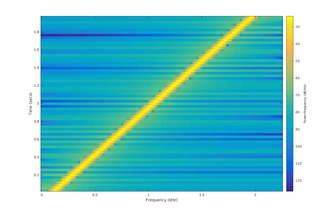
الگو:Listen در یک چرپ فرکانس خطی یا به سادگی چرپ خطی، فرکانس لحظه‌ای $f(t)$ دقیقاً به صورت خطی با زمان تغییر می‌کند: $$f(t)=ct+f_0,$$

در اینجا $f_0$ فرکانس شروع (در زمان $t=0$) و $c$ نرخ چرپ، ثابت فرض شده است:$$c=\frac{f_1-f_0}{T}=\frac{\mathrm{\Delta }f}{\mathrm{\Delta }t}.$$اینجا، $f_1$ فرکانس نهایی است و $T$ زمان لازم برای جاروب کردن از $f_0$ به الگو:Nowrap است.

تابع حوزه-زمان متناظر برای فاز هر سیگنال نوسانی، انتگرال تابع فرکانس است، زیرا انتظار می‌رود فاز مانند $\varphi (t+\mathrm{\Delta }t)\simeq \varphi (t)+2\pi f(t)\mathrm{\Delta }t$ رشد کند؛ یعنی مشتق فاز فرکانس زاویه ای ${\varphi }^{\prime }(t)=2\pi f(t)$ است.

برای چیپ خطی، این نتیجه به شرح زیر است:$$\begin{array}{cc}\varphi (t)& ={\varphi }_0+2\pi \underset{0}{\overset{t}{\int }}f(\tau )d\tau \\ & ={\varphi }_0+2\pi \underset{0}{\overset{t}{\int }}(c\tau +f_0)d\tau \\ & ={\varphi }_0+2\pi (\frac{c}{2}{t}^2+f_{0}t),\end{array}$$در اینجا ${\varphi }_0$ فاز اولیه (در زمان $t=0$) است؛ بنابراین به این سیگنال فاز درجه‌دوم نیز می‌گویند.

تابع حوزه زمان متناظر برای یک چرپ خطی سینوسی، سینوسِ فاز برحسب رادیان است:$$x(t)=\sin [{\varphi }_0+2\pi (\frac{c}{2}{t}^2+f_{0}t)]$$الگو:پاک‌کن

نمایی

شکل موج چرپ نمایی. یک موج سینوسی که در طول زمان به صورت تصاعدی فرکانس افزایش می‌یابد

الگو:Listen در یک چرپ هندسی، که به آن چرپ نمایی نیز می‌گویند، فرکانس سیگنال با یک رابطه هندسی در طول زمان تغییر می‌کند. به عبارت دیگر، اگر دو نقطه در شکل موج انتخاب شود، $t_1$ و $t_2$ ، و فاصله زمانی بین آنها $T=t_2-t_1$ ثابت نگه داشته شده، نسبت فرکانس $f\left(t_2\right)/f\left(t_1\right)$ نیز ثابت خواهد بود.

در یک چیپ نمایی، فرکانس سیگنال به صورت نمایی بر حسب زمان تغییر می‌کند:$$f(t)=f_0{k}^{\frac{t}{T}}$$در اینجا $f_0$ فرکانس شروع (در $t=0$) و $k$ نرخ تغییر نمایی فرکانس است. برخلاف چرپ خطی که دارای چرپینگی ثابت است، چرپ نمایی دارای نرخ فرکانس افزایشی نمایی است.$$k={\left(\frac{f_1}{f_0}\right)}^{\frac{T}{t}}$$تابع حوزه زمان متناظر برای فاز یک چیپ نمایی، انتگرال فرکانس است:$$\begin{array}{cc}\varphi (t)& ={\varphi }_0+2\pi \underset{0}{\overset{t}{\int }}f(\tau )d\tau \\ & ={\varphi }_0+2\pi f_0\underset{0}{\overset{t}{\int }}{k}^{\frac{\tau }{T}}d\tau \\ & ={\varphi }_0+2\pi f_0\left(\frac{k^{\frac{t}{T}}-1}{\ln (k)}\right)\end{array}$$اینجا ${\varphi }_0$ فاز اولیه ا (در $t=0$) ست.

تابع حوزه زمان متناظر برای یک چیپ نمایی سینوسی، سینوس فاز برحسب رادیان است:$$x(t)=\sin [{\varphi }_0+2\pi f_0\left(\frac{k^{\frac{t}{T}}-1}{\ln (k)}\right)]$$همان‌طور که برای چرپ خطی بود، فرکانس لحظه‌ای چرپ نمایی از فرکانس اساسی $f(t)=f_0{k}^{\frac{t}{T}}$ همراه با هارمونیک‌های اضافی تشکیل شده است. الگو:مدرک

هذلولی

چرپ‌های هذلولی در کاربردهای رادار استفاده می‌شود، زیرا حداکثر پاسخ فیلتر تطبیق‌شده را پس از اعوجاج توسط اثر داپلر نشان می‌دهند.

در یک چرپ هذلولی، فرکانس سیگنال به صورت هذلولی برحسب زمان تغییر می‌کند:$$f(t)=\frac{f_0{f}_{1}T}{(f_0-f_1)t+f_{1}T}$$تابع حوزه زمان متناظر برای فاز یک چرپ هذلولی، انتگرال فرکانس است:$$\begin{array}{cc}\varphi (t)& ={\varphi }_0+2\pi \underset{0}{\overset{t}{\int }}f(\tau )d\tau \\ & ={\varphi }_0+2\pi \frac{-f_0{f}_{1}T}{f_1-f_0}\ln (1-\frac{f_1-f_0}{f_{1}T}t)\end{array}$$دراینجا ${\varphi }_0$ فاز اولیه (در $t=0$) است.

تابع حوزه زمانی متناظر برای یک چرپ هذلولی سینوسی، سینوس فاز برحسب رادیان است:$$x(t)=\sin [{\varphi }_0+2\pi \frac{-f_0{f}_{1}T}{f_1-f_0}\ln (1-\frac{f_1-f_0}{f_{1}T}t)]$$

تولید

یک سیگنال چرپ را می‌توان با مدار آنالوگ از طریق یک نوسان‌ساز کنترل‌شده با ولتاژ (VCO) و یک ولتاژ کنترلی به صورت خطی یا نمایی تولید کرد. همچنین می‌توان آن را به صورت دیجیتالی توسط یک پردازنده سیگنال دیجیتال (DSP) و مبدل دیجیتال به آنالوگ (DAC)، با استفاده از یک ترکیب‌کننده دیجیتالی مستقیم (DDS) و با تغییر گام در نوسانگر عددی کنترل‌شده تولید کرد. همچنین می‌تواند توسط یک نوسانگر YIG تولید شود.

تغییر در فرکانس کد مورس از فرکانس مورد نظر، به دلیل پایداری ضعیف در نوسانگر RF، به عنوان چرپ شناخته می‌شود، و در سامانه آراس‌تی یک حرف ضمیمه C داده می‌شود.

جستارهای وابسته

• طیف چرپ
• فشرده‌سازی چرپ
• طیف گسترده چرپ
• آینه جیرپ
• تقویت پالس چرپ
• تبدیل چرپلت
• رادار موج پیوسته
• پاشش (اپتیک)
• فشرده‌سازی پالس
• الگو:پیوند بخش

پیوند به بیرون

• مولد آنلاین تن چرپ (خروجی فایل WAV)
• سونار CHIRP در فیش‌فایندر
• سونار CHIRP در فیش‌فایندر