مدل کاکس-اینگرسول-راس

Three trajectories of CIR Processes

در ریاضیات مالی، مدل کاکس-اینگرسول-راس الگو:به انگلیسی (یا مدل CIR) مدل سازی نرخ بهره را توصیف می‌کند. این مدل، یک نوع «مدل تک عاملی» (مدل نرخ بهره کوتاه مدت) است که تغییرات نرخ بهره را با توجه به یک نوع از ریسک بازار توصیف می‌کند. این مدل می‌تواند در ارزیابی نرخ بهره اوراق مشتقه استفاده شود. این مدل در سال ۱۹۸۵ توسط جان سی کاکس، جاناتان. اینگرسول و استفان. راس به عنوان توسعه‌ای از مدل Vasicek معرفی شد.

مدل

CIR process

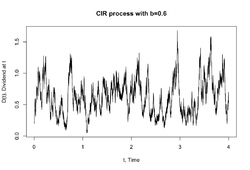
مدل CIR نرخ بهره آنی را از طریق معادله دیفرانسیل تصادفی زیر که به فرایند CIR معروف است؛ تعیین می‌کند:

$d{r}_t=a(b-r_t)dt+\sigma \sqrt{r_t}d{W}_t$

که W_t در آن یک فرایند وینر (مدل سازی عامل ریسک بازار به صورت تصادفی) و a، b و سیگما، پارامترهای آن هستند. پارامتر a مربوط به رابطه تنظیم سرعت، پارامتر b میانگین و سیگما شدن نوسان پذیری است. عامل انحراف، $a(b-r_t)$ است که دقیقاً همان مدل Vasicek است. این تضمین می‌کند که بازگشت به میانگین نرخ بهره به سمت ارزش بلندمدت b، با سرعت تعدیل شده توسط پارامتر مثبت a. عامل انحراف استاندارد، سیگما، تابع (r-t)، امکان نرخ بهره منفی برای همه ارزش‌های مثبت a و b را محدود می‌کند. نرخ بهره صفر نیز محدود می‌شود اگر شرط 2ab≥σ^۲ برقرار باشد. به‌طور کلی، زمانی که نرخ بهره در پایین‌ترین سطح (نزدیک به صفر)، انحراف استاندارد (واریانس) نیز بسیار کوچک می‌شود که تعدیل اثر شوک تصادفی روی نرخ دارد به تبع آن وقتی که نرخ به سمت صفر میل می‌کند، مدلسازی آن توسط عامل انحراف، نرخ را به سمت بالا هدایت می‌کند (به سمت تعادل). این فرایند را می‌توان به عنوان مجموع مربع فرایند Ornstein–Uhlenbeck تعریف کرد..CIR یک فرایند تخصصی است و دارای یک توزیع ثابت است. همین روند در مدل Heston، تحت مدل نوسانات تصادفی استفاده می‌شود.

توزیع

توزیع آتی توزیع ارزش آتی تحت مدل CIR به صورت فرمول زیر محاسبه می‌شود:

$r_{t+T}=\frac{Y}{2c}$،

که در آن $c=\frac{2a}{(1-e^{-aT}){\sigma }^2}$ و Y یک توزیع مجذور کای دو و غیر مرکزی با $\frac{4ab}{{\sigma }^2}$ درجه آزادی و پارامتر غیر مرکزی $2c{r}_t{e}^{-aT}$. به‌طور مشخص، تابع چگالی احتمال به صورت زیر است:

$f(r_{t+T};r_t,a,b,\sigma )=c{e}^{-u-v}{\left(\frac{v}{u}\right)}^{q/2}{I}_q(2\sqrt{uv})$،

که در آن $q=\frac{2ab}{{\sigma }^2}-1$، $u=c{r}_t{e}^{-aT}$، $v=c{r}_{t+T}$ و $I_q(2\sqrt{uv})$ که تابع در آن بسته به اولین نوع سفارش q اصلاح شده‌است.

توزیع مجانبی

با توجه به خاصیت بازگشت به میانگین، از آنجایی که زمان زیاد می‌شود، توزیع r_∞ یک توزیع گاما با چگالی احتمالی نزدیک به:

$f(r_{\mathrm{\infty }};a,b,\sigma )=\frac{{\omega }^{\nu }}{\mathrm{\Gamma }(\nu )}{r}_{\mathrm{\infty }}^{\nu -1}{e}^{-\omega r_{\mathrm{\infty }}}$،

که در آن $\omega =2a/{\sigma }^2$ و $\nu =2ab/{\sigma }^2$ است.

درجه‌بندی

حداقل مربعات معمولی SDE پیوسته می‌تواند به شرح زیر گسسته باشد. $r_{t+\mathrm{\Delta }t}-r_t=a(b-r_t)\mathrm{\Delta }t+\sigma \sqrt{r_t\mathrm{\Delta }t}{ϵ}_t$، که معادل است $\frac{r_{t+\mathrm{\Delta }t}-r_t}{{\sqrt{r}}_t}=\frac{ab\mathrm{\Delta }t}{{\sqrt{r}}_t}-a{\sqrt{r}}_t\mathrm{\Delta }t+\sigma \sqrt{\mathrm{\Delta }t}{ϵ}_t$، این معادله می‌تواند برای رگرسیون خطی استفاده شود.

قیمت گذاری اوراق قرضه

تحت فرض نبود آربیتراژ، اوراق قرضه می‌تواند با استفاده از فرایند نرخ بهره قیمت گذاری شود. قیمت اوراق قرضه نمایه از نرخ بهره است:

$P(t,T)=A(t,T)\exp (-B(t,T)r_t)$

که در آن

$A(t,T)={\left(\frac{2h\exp ((a+h)(T-t)/2)}{2h+(a+h)(\exp ((T-t)h)-1)}\right)}^{2ab/{\sigma }^2}$

$B(t,T)=\frac{2(\exp ((T-t)h)-1)}{2h+(a+h)(\exp ((T-t)h)-1)}$

$h=\sqrt{a^2+2{\sigma }^2}$

Extensions

Time varying functions replacing coefficients can be introduced in the model in order to make it consistent with a pre-assigned term structure of interest rates and possibly volatilities. The most general approach is in Maghsoodi (1996). A more tractable approach is in Brigo and Mercurio (2001b) where an external time-dependent shift is added to the model for consistency with an input term structure of rates. A significant extension of the CIR model to the case of stochastic mean and stochastic volatility is given by مدل چن (1996) and is known as مدل چن. A CIR process is a special case of a basic affine jump diffusion, which still permits a closed-form expression for bond prices.

جستارهای وابسته

• Hull-White model
• مدل واسیچک
• مدل چن

منابع

• الگو:Cite book
• الگو:Cite journal
• الگو:Cite journal
• الگو:Cite book
• الگو:Cite journal
• de:Wurzel-Diffusionsprozess#Cox-Ingersoll-Ross-Modell