حرکت هارمونیک ساده

الگو:Sidebar with collapsible lists در مکانیک و فیزیک نوسانگر هماهنگ ساده نمونه‌ای از یک حرکت نوسانی است. این حرکت می‌تواند به عنوان مدل ریاضی برای انواع حرکت‌ها به کار رود به خصوص در حرکت‌های تناوبی. به علاوه پدیده دیگری که می‌توان با نوسانگر هماهنگ ساده تقریب زده شود ارتعاش مولکولی است. نوسانگر هماهنگ ساده با حرکت وزنه متصل به فنر ایجاد می‌شود.

بررسی اولیه

نوسانگر هماهنگ ساده

یک نوسانگر

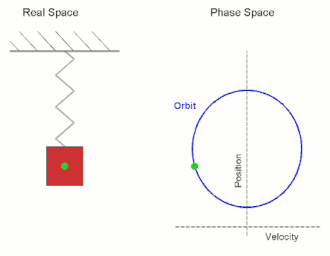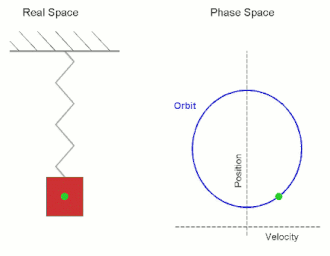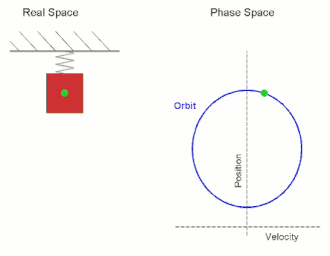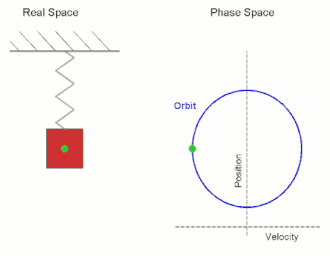
در تصویر متحرک روبه رو یک نوسانگر هماهنگ را می‌بینید که از یک فنر متصل به جسم ثابت (سقف) و یک جسم متحرک تشکیل شده‌است. اگر جسم را در نقطه تعادلی رها شود حرکتی رخ نمی‌دهد ولی اگر کمی از حالت تعادلی خارج شود به آن نیرو وارد شده و شروع به نوسان می‌کند. طبق قانون هوک: $𝐅=-k𝐱$ که F نیرو و k ضریب سختی است.

دینامیک نوسانگر هماهنگ ساده

معادله نوسانگر هماهنگ ساده یک بعدی که یک معادله دیفرانسیل معمولی مرتبه دو است و ضرایب ثابت دارد می‌تواند با استفاده از قانون دوم نوشته شود: $F_{net}=m\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}=-kx$ پس حال می‌توان گفت که :$\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}=-\left(\frac{k}{m}\right)x$ حل این معادله دیفرانسیل یک موج سینوسی به این صورت است:$x(t)=x_0\cos \left(\omega t\right)+\frac{v_0}{\omega }\sin \left(\omega t\right)$ که می‌تواند به این صورت نوشته شود:$x(t)=A\cos (\omega t+\phi )$ که در آن:

$\omega =\sqrt{\frac{k}{m}}$ و $A=\sqrt{{c_1}^2+{c_2}^2}$ و $\tan \phi =\left(\frac{c_2}{c_1}\right)$

در نتیجه:

$v(t)=\frac{\mathrm{d}x}{\mathrm{d}t}=-A\omega \sin (\omega t-\phi )$

که الگو:Nowrap

$f=\frac{1}{2\pi }\sqrt{\frac{k}{m}}$

الگو:Nowrap که T دوره تناوب است

$T=2\pi \sqrt{\frac{m}{k}}$

انرژی

یک آونگ که حرکت آن شبیه به نوسانگر هماهنگ ساده است

$k/m$ را به جای ${\omega }^2$ جاگذاری می‌کنیم پس انرژی جنبشی:

$K(t)=\frac{1}{2}m{v}^2(t)=\frac{1}{2}m{\omega }^2{A}^2{\sin }^2(\omega t-\phi )=\frac{1}{2}k{A}^2{\sin }^2(\omega t-\phi )$

و انرژی پتانسیل : $U(t)=\frac{1}{2}k{x}^2(t)=\frac{1}{2}k{A}^2{\cos }^2(\omega t-\phi )$

و انرژی مکانیکی مقدار ثابتی دارد : $E=K+U=\frac{1}{2}k{A}^2$

منابع

• الگو:Cite book
• الگو:Cite book
• الگو:Cite book
• الگو:Cite book