کد گری
الگو:ویکیسازینمایش کدهای دودویی که بعد از فرانک گری (Frank Gray) به نام کد گِرِی شناخته شد، یک سیستم از اعداد دودویی است که هر دو عدد متوالی فقط در یک بیت با هم اختلاف داشته باشند. امروزه کدگری به طورِ گسترده برای تصحیحِ اشکالات در سیستم ارتباط دیجیتالی مثل تلویزیون کابلی و تلویزیون دیجیتال استفاده میشود.
نام
یکی از محققان آزمایشگاه بل (Bell) به نام فرانک گری اولین بار بهطور رسمی کد گری را مورد استفاده قرار داد و این کد بعد از گری توسط افرادی که از آن استفاده میکردند کد گری نامگذاری شد.
تاریخچه و کاربردهای علمی
کد گری قبل از آن که در مهندسی به کار رود در پازلهای ریاضی به کار برده میشد، ریاضیدان فرانسوی Emile Boudat از کد گری در سال ۱۸۷۸در تلگراف استفاده کرد و برای این کارش مدال دریافت کرد.
و اما کاربردهای آن، از کد گری به عنوان یک رمزگذار استفاده میشود که نسبت به رمزگذار عادی برتری دارد.
در نمایش کد گری خاصیت دایرهای بودن آن باعث میشود که دو عدد دو سر نیز فقط در یک بیت متفاوت باشند.
کد گری یک دور همیلتونی در یک مکعب بعدی تولید میکند که هر کدام از اعداد آن یک راس را نشان میدهد و نیز در الگوریتمهای ژنتیکی از آن استفاده میشود و البته برچسب گذاری جدول کارنو از موارد دیگر استفاده آن است.
زمانی کد گری برای آدرس دهی حافظه در کامپیوتر استفاده میشود، کامپیوتر نیروی کمتری صرف یافتن آدرسها میکند چون هر آدرس با قبلی فقط در یک بیت متفاوت است.
طراحان مدارهای منطقی از کد گری بهطور گسترده برای عبور چند بیت اطلاعات بین سیستمهای همزمان استفاده میکنند.
انگیزهٔ پیدایش کد گری
بعضی از دستگاهها وضعیت دستگاه را با کدهای باینری نمایش میدهند، اگر این دستگاهها از کد باینری عادی استفاده کند این دو وضعیت پشت سر هم خواهند بود الگو:چپچین..
۰۱۱
۱۰۰...
الگو:پایان چپچین و مشکل کد باینری عادی این است که در حالت طبیعی خیلی بعید است که چند بیت همزمان تغییر کنند همانطور که در بالا نمایش داده شدهاست که در کد باینری عادی هر سه بیت همزمان تغییر کردهاند اما میتوان اعداد را طوری در کنار هم قرار داد که فقط در یک بیت متفاوت باشند و تغییر زیادی نکنند مثل پس کد باینری منعکس شده یا همان کد گری این مشکل را حل میکند زیرا که فقط یک بیت در آنها تغییر میکند. الگو:چپچین Gray Binary الگو:سخ۰ ۰۰۰ ۰۰۰ الگو:سخ۱ ۰۰۱ ۰۰۱ الگو:سخ۲ ۰۱۱ ۰۱۰ الگو:سخ۳ ۰۱۰ ۰۱۱ الگو:سخ۴ ۱۱۰ ۱۰۰ الگو:سخ۵ ۱۱۱ ۱۰۱ الگو:سخ۶ ۱۰۱ ۱۱۰الگو:سخ ۷ ۱۰۰ ۱۱۱
الگو:پایان چپچین با توجه به حالت ۷ و ۰ میبینیم که فقط در یک بیت تفاوت دارند که همان خاصیت دورهای یا چرخشی بودن کد گری میگوییم.
ساختن کد گری بیتی
یک کد گری بیتی را میتوان به صورت بازگشتی تولید کرد، به این شکل که یک لیست بیتی داریم آن را وارونه میکنیم (خط افقی در شکل زیر مانند آینه عمل کند) و در انتهای لیست اصلی میچسبانیم و سپس در ابتدای لیست اول و در ابتدای لیست دوم قرار میدهیم مثلاً برای کد گری یک بیتی ، را داریم (البته میتوان از کد گری بیتی هم استفاده کرد). ، و بعد با آن کد گری بیتی را به صورت بازگشتی بسازیم و اکنون شبه کد آن را داریم.
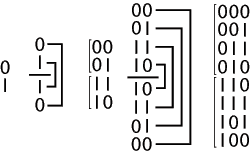
الگوریتم کد گری
ابتدا یک الگوریتم برای تبدیل کد باینری عادی به کد گری وجود دارد. الگو:چپچین ۱ Let B[n:0] be the input array of bits in the usual binary representation, [0] being LSB الگو:سخ۲ Let G[n:0] be the output array of bits in Gray code الگو:سخ۳ G[n] = B[n] الگو:سخ۴ for i = n-1 downto 0 الگو:سخ۵ G[i] = B[i+1] XOR B[i] الگو:پایان چپچین
الگوریتم تبدیل کد گری به کد باینری
الگو:چپچین ۱ Let G[n:0] be the input array of bits in Gray code الگو:سخ۲ Let B[n:0] be the output array of bits in the usual binary representation الگو:سخ۳ B[n] = G[n] الگو:سخ۴ for i = n-1 downto 0 الگو:سخ۵ B[i] = B[i+1] XOR G[i] الگو:پایان چپچین
الگوریتم تبدیل کد باینری به گری
اول از همه کد باینری عدد مورد نظر را مینویسیم
سپس از سمت چپ شروع میکنیم و اولین عدد را همانطور که هست نوشته سپس دوتا دوتا عددها رو مقایسه میکنیم، اگر هردو یکسان باشند در این صورت به جای آن دو عدد صفر میگذاریم، در غیر این صورت: یعنی اگر یکی از عددها صفر و دیگری یک باشد، آن وقت به جای آن دو عدد یک را به جای آنها مینویسیم
برای مثال
۷ باینری>> ۱ ۱ ۱ ۰
۷ گری>> ۰ ۰ ۱ ۰
یک الگوریتم سریع درC/java به شکل زیر است
الگو:چپچین ۱ long inverseGray(long n) { الگو:سخ۲ long ish, ans, idiv; الگو:سخ۳ ish = ۱; الگو:سخ۴ ans = n; الگو:سخ۵ while(true) { الگو:سخ۶ idiv = ans>> ish; الگو:سخ۷ ans ^= idiv; الگو:سخ۸ if (idiv <= ۱ || ish == ۳۲) الگو:سخ۹ return ans; الگو:سخ۱۰ ish <<= ۱; // double number of shifts next time}الگو:سخ} الگو:پایان چپچین
کد گری n تایی
انواع مختلفی از کد گری وجود دارد که یی از این انواع مختلف کد گری n تایی است که به عنوان کد گری غیر دوتایی (۰و۱)هم شناخته میشود یعنی به غیر از ۰ و ۱ از اعداد دیگر هم استفاده میشود (همانطور که نام آن نشان میدهد) و در رمزگذاری هم از آن استفاده میشود. برای مثال یک کد گری سه تایی از بیتهای {۰و۱و۲} استفاده میکند. کد گری سه تایی الگو:چپچین
،۰۰۰ ،۰۰۱ ،۰۰۲ ،۰۱۲ ،۰۱۱ ،۰۱۰ ،۰۲۰ ،۰۲۱ ،۰۲۲ ،۱۲۲ ،۱۲۱ ،۱۲۰ ،۱۱۰ ،۱۱۱ ،۱۱۲ ،۱۰۲ ،۱۰۱ ،۱۰۰ ،۲۰۰ ،۲۰۱ ،۲۰۲ ،۲۱۲ ،۲۱۱ ،۲۱۰ ،۲۲۰ ،۲۲۱ ،۲۲۲ الگو:پایان چپچین
یک کد گری (n,k)تایی یک کد گری n تایی است که دارای k بیت است مثلاً یک کد گری(۲و۳)برابر است با {۰۰، ۰۱، ۰۲، ۱۲، ۱۱، ۱۰، ۲۰، ۲۱، ۲۲} و اکنون الگوریتم ساخت کد گری (n,k) در C/java در زیر آمدهاست
الگو:چپچین
الگو:سخint n[k+1]; // stores the maximum for each digit الگو:سخint g[k+1]; // stores the Gray code الگو:سخint u[k+1]; // stores +1 or -1 for each element الگو:سخint i, j; الگو:سخ// initialize values الگو:سخfor(i = ۰; i <= k; i++) { الگو:سخg[i] = ۰; الگو:سخu[i] = ۱; الگو:سخn[i] = N; الگو:سخ} الگو:سخ// generate codes الگو:سخwhile(g[k] == ۰) { الگو:سخ// at this point (g[۰],... ,g[k-1]) hold a subsequent element of the (N,k)-Gray code الگو:سخi = ۰; الگو:سخj = g[۰] + u[0]; الگو:سخwhile((j>= n[i]) || (j <۰)) { الگو:سخu[i] = -u[i]; الگو:سخi++; الگو:سخj = g[i] + u[i]; الگو:سخ} g[i] = j; } الگو:سخالگو:پایان چپچین
اما یادآور میشویم که کد گری (n,k)تایی برای nهای فرد خاصیت چرخشی را حفظ نمیکنند ولی برای nهای زوج خاصیت چرخشی را حفظ میکنند.
پیوند بیشتر
- "Gray Code" demonstration by Michael Schreiber, The Wolfram Demonstrations Project (with Mathematica implementation). 2007.
- NIST Dictionary of Algorithms and Data Structures: Gray code
- Numerical Recipes in C, section 20.2 describing Gray codes in detail
- Single-Track Circuit Codes by Hiltgen, Alain P.; Paterson, Kenneth G. الگو:Webarchive
منابع
- Black, Paul E. Gray code. 25 February 2004. NIST
- Savage, Carla. "A Survey of Combinatorial Gray Codes." Society of Industrial and Applied Mathematics Review 39 (1997): 605–629.
- Wilf, Herbert S. Combinatorial algorithms: an update, SIAM, 1989, الگو:ISBN. Chapters 1-3.
- A Gray code implementation in Java to convert decimals
