پیش‌نویس:گروه دووجهی بی‌نهایت

p1m1, (*∞∞)	p2, (22∞)	p2mg, (2*∞)
الگو:سخ	الگو:سخ	الگو:سخ
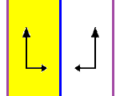
در یک صفحه دوبعدی، سه گروه فرایز p1m1،p2 و p2mg شبیه به گروه دووجهی نامتناهی هستند. همه آنها دو مولد دارند. اولی دارای دو خط بازتابی موازی است، دومی دارای دو دو خط چرخشی تاشو، و آخری یک آیینه و دو خط چرخشی تاشو

در ریاضیات،گروه دووجهی نامتناهی یک گروه نامتناهی با ویژگی‌های مشابه گروه دووجهی متناهی است.

در هندسه اقلیدسی، گروه دووجهی نامتناهی، تقارن گروه فرایز (خط‌های تکرار شونده موازی) را نشان می‌دهد. در تصویر روبه‌رو p1m۱، به عنوان مجموعه ای نامتناهی از بازتاب‌های موازی در امتداد یک محور دیده می‌شود.

تعریف

یک گروه دووجهی، با یکبار چرخش r و یکبار بازتاب ایجاد می‌شود. اگر چرخشی مضربی گویا و غیرگنگ چرخش کاملی باشد، آنگاه هر چند n صحیحی وجود داشته باشد،rⁿ هویت وی خواهد بود و ما یک گروه نامتناهی دووجهی از مرتبه ۲n خواهیم داشت. اگر چرخش مضرب گویای چرخشی کامل نباشد، چنین nی وجود ندارد و گروه به‌دست آمده، عناصر نامتناهی زیادی خواهد داشت و گروه نامتناهی دووجهی نامیده می‌شود.

ارائه ان به این صورت است: $⟨r,s\mid s^2=1,srs=r^{-1}⟩$$⟨x,y\mid x^2=y^2=1⟩$