مدول تزریقی

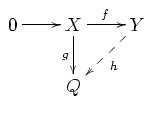
مدول تزریقی الگو:به انگلیسی در ریاضیات، بخصوص در شاخه‌ای از جبر مجرد به‌نام نظریه مدول‌ها، یک مدولی چون $Q$ است که در خواص مهمی با $ℤ$ -مدول $ℚ$ ، یعنی اعداد گویا با در نظر گرفتن ساختار $ℤ$ -مدولی، مشترک است. بخصوص، اگر $Q$ زیر مدولی از یک مدول دیگر باشد، آنگاه جمعوند مستقیمی از آن مدول خواهد بود؛ همچنین، اگر زیر مدولی از یک مدول $Y$ داده شده باشد، آنگاه هر همریختی مدولی از این زیر مدول به $Q$ را می توان به همریختی از تمام $Y$ به $Q$ توسعه داد. این مفهوم دوگان مدول های تصویری است. مدول های تزریقی در الگو:Harv معرفی شدند و به عنوان مثال در کتاب الگو:Harv به طور دقیق مورد بحث قرار گرفته است.

مدول های تزریقی به طور گسترده مورد مطالعه قرار گرفته و مفاهیم متنوع دیگری بر اساس آن ها تعریف شده اند مثل این موارد: هم-مولدهای تزریقی الگو:به انگلیسی مدول های تزریقی اند که وفادارانه کل رسته مدول ها را نمایش می دهند. تحلیل تزریقی الگو:به انگلیسی میزان دور بودن یک مدول از تزریقی بودن را بر حسب بعد تزریقی آن سنجیده و مدول ها را در رسته مشتق شده الگو:به انگلیسی نمایش می دهد. پوسته تزریقی الگو:به انگلیسی توسیع های اساسی الگو:به انگلیسی بیشینه (ماکسیمال) اند و مشخص می شود که این اشیاء توسیع های تزریقی کمینه (مینیمال) اند. هر مدول تزریقی روی یک

در ریاضیات، بخصوص در شاخه ای از جبر مجرد به نام نظریه مدول‌ها، یک مدول تزریقی الگو:به انگلیسی مدولی چون $Q$ است که در خواص مهمی با $ℤ$ -مدول $ℚ$ ، یعنی اعداد گویا با در نظر گرفتن ساختار $ℤ$ -مدولی، مشترک است. بخصوص، اگر $Q$ زیر مدولی از یک مدول دیگر باشد، آنگاه جمعوند مستقیمی از آن مدول خواهد بود؛ همچنین، اگر زیر مدولی از یک مدول $Y$ داده شده باشد، آنگاه هر همریختی مدولی از این زیر مدول به $Q$ را می توان به همریختی از تمام $Y$ به $Q$ توسعه داد. این مفهوم دوگان مدول های تصویری است. مدول های تزریقی در الگو:Harv معرفی شدند و به عنوان مثال در کتاب الگو:Harv به طور دقیق مورد بحث قرار گرفته است.

مدول های تزریقی به طور گسترده مورد مطالعه قرار گرفته و مفاهیم متنوع دیگری بر اساس آن ها تعریف شده اند مثل این موارد: هم-مولدهای تزریقی الگو:به انگلیسی مدول های تزریقی اند که وفادارانه کل رسته مدول ها را نمایش می دهند. تحلیل تزریقی الگو:به انگلیسی میزان دور بودن یک مدول از تزریقی بودن را بر حسب بعد تزریقی آن سنجیده و مدول ها را در رسته مشتق شده الگو:به انگلیسی نمایش می دهد. پوسته تزریقی الگو:به انگلیسی توسیع های اساسی الگو:به انگلیسی بیشینه (ماکسیمال) اند و مشخص می شود که این اشیاء توسیع های تزریقی کمینه (مینیمال) اند. هر مدول تزریقی روی یک حلقه نوتری را می توان به طور منحصر به فردی به صورت جمع مستقیم مدول های تجزیه-ناپذیر نوشت، بنابر این روی چنین حلقه هایی ساختار مدول های تزریقی به خوبی درک شده است. ممکن است یک مدول روی یک حلقه تزریقی باشد ولی روی حلقه دیگری تزریقی نباشد، اما روش هایی برای تغییر حلقه در مدول ها وجود دارند که به خوبی شناخته شده و حالت های خاص را می توان با آن روش ها مدیریت کرد. حلقه هایی که خود مدول های تزریقی اند، خواص جالبی دارند، از جمله این حلقه ها، حلقه هایی چون حلقه های گروهی الگو:به انگلیسی از گروه های متناهی روی میدان ها می باشد. مدول های تزریقی شامل گروه های تقسیم‌پذیر بوده و توسط مفهوم اشیاء تزریقی در نظریه رسته‌ها تعمیم پیدا می کنند.