دوپاره‌سازی قطب

دوپاره‌سازی قطب الگو:به انگلیسی یا مجزاسازی قطب پدیده‌ای است که در برخی از اشکال جبران‌سازی فرکانس مورد استفاده در تقویت‌کننده‌های الکترونیکی بکار گرفته می‌شود. هنگامی که یک خازن بین دو طرف ورودی و خروجی تقویت‌کننده با هدف جابجایی پایین‌ترین قطب در فرکانس (معمولا یک قطب ورودی) به فرکانس‌های پایین‌تر وارد می‌شود، دوپاره‌سازی قطب باعث می‌شود که قطب بعدی در فرکانس (معمولا یک قطب خروجی) به فرکانس بالاتر حرکت کند. این حرکت قطب پایداری تقویت‌کننده را افزایش می‌دهد و پاسخ پله آن را به قیمت کاهش سرعت بهبود می‌بخشد.^[۱]^[۲]^[۳]^[۴]

نمونه‌ای از دوپاره‌سازی قطب

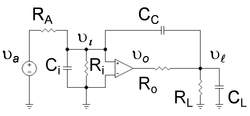
این مثال نشان می‌دهد که واردکردن خازن به نام C_C در تقویت‌کننده شکل ۱ دو نتیجه دارد: اول باعث می‌شود پایین‌ترین قطب فرکانسی تقویت‌کننده همچنان در فرکانس پایین‌تر حرکت کند و دوم اینکه باعث می‌شود قطب بالاتر به سمت بالاتر در فرکانس حرکت کند.^[۵] تقویت‌کننده شکل ۱ دارای یک قطب فرکانس پایین به دلیل مقاومت ورودی R_i و ظرفیت‌خازنی C_i اضافه شده با ثابت زمانی C_i (R_A || R_i) است. این قطب در فرکانس توسط اثر میلر به پایین منتقل می‌شود. با افزودن مقاومت بار R_L و ظرفیت‌خازنی C_L با ثابت زمانی C_L(R_o || R_L) به تقویت‌کننده یک قطب خروجی فرکانس بالا داده می‌شود. حرکت رو به بالا قطب فرکانس-بالا به این دلیل رخ می‌دهد که خازن جبران‌سازی تقویت‌شدهٔ-میلری C_C وابستگی فرکانس تقسیم‌کننده ولتاژ خروجی را تغییر می‌دهد.

با عطف به هدف دوم، نشان دادن حرکت قطب بالاتر همچنان در فرکانس بالاتر، لازم است به سمت خروجی مدار نگاه کنید، که عامل دومی را به بهره کلی و وابستگی فرکانس اضافی کمک می‌کند. ولتاژ $v_{o}$ با بهره آپ‌امپ ایده‌آل در داخل تقویت‌کننده تعیین می‌شود

\frac{v_{ℓ}}{v_{i}} = A_{v} \frac{R_{L}}{R_{L} + R_{o}}

\cdot \frac{1 + j ω C_{C} R_{o} / A_{v}}{1 + j ω (C_{L} + C_{C}) (R_{o} ‖ R_{L})} .

که یک رول آف با فرکانس شروع از f₁ را نشان می‌دهد که در آن

\begin{matrix} f_{1} & = \frac{1}{2 π (C_{M} + C_{i}) (R_{A} ‖ R_{i})} \\ = \frac{1}{2 π τ_{1}} \end{matrix}

که $τ_{1}$ نشانه گذاری برای ثابت زمانی پایین‌ترین قطب را معرفی می‌کند. این فرکانس کمتر از فرکانس پایین اولیه تقویت‌کننده است که برای C_C = 0 F است $\frac{1}{2 π C_{i} (R_{A} ‖ R_{i})}$ .

هدف اول، برای نشان دادن پایین‌ترین قطب از نظر فرکانس به سمت پایین، با استفاده از رویکردی مشابه با مقاله قضیه میلر ایجاد می‌شود. طبق روشی که در مقاله دربارهٔ قضیه میلر توضیح داده شد، مدار شکل ۱ به مدار شکل ۲ تبدیل می‌شود که از نظر الکتریکی معادل شکل ۱ است. استفاده از قانون جریان کریشهف در سمت ورودی شکل ۲ ولتاژ ورودی را تعیین می‌کند. $v_{i}$ به تقویت‌کننده عملیاتی ایده‌آل به عنوان تابعی از ولتاژ سیگنال اعمال شده $v_{a}$ ، یعنی

v_{o} = A_{v} v_{i} .

با استفاده از این رابطه و اعمال قانون جریان کریشهف در سمت خروجی مدار، ولتاژ بار را تعیین می‌کند. $v_{ℓ}$ به عنوان تابعی از ولتاژ $v_{i}$ در ورودی آپ‌امپ ایده‌آل به صورت:

\frac{v_{ℓ}}{v_{i}} = A_{v} \frac{R_{L}}{R_{L} + R_{o}}

\cdot \frac{1 + j ω C_{C} R_{o} / A_{v}}{1 + j ω (C_{L} + C_{C}) (R_{o} ‖ R_{L})} .

این عبارت با ضریب بهره که قبلاً برای سمت ورودی مدار پیدا شده بود ترکیب می‌شود تا بهره کلی را به دست آورد

\frac{v_{ℓ}}{v_{a}} = \frac{v_{ℓ}}{v_{i}} \frac{v_{i}}{v_{a}}

= A_{v} \frac{R_{i}}{R_{i} + R_{A}} \cdot \frac{R_{L}}{R_{L} + R_{o}}

\cdot \frac{1}{1 + j ω (C_{M} + C_{i}) (R_{A} ‖ R_{i})}

\cdot \frac{1 + j ω C_{C} R_{o} / A_{v}}{1 + j ω (C_{L} + C_{C}) (R_{o} ‖ R_{L})} .

به نظر می‌رسد این فرمول بهره یک پاسخ دوقطبی ساده با دو ثابت زمانی را نشان می‌دهد. (همچنین یک صفر در صورت نشان می‌دهد، اما با فرض اینکه بهره تقویت‌کننده A_v بزرگ است، این صفر فقط در فرکانس‌های بسیار بالا که در این بحث اهمیت ندارد، مهم است، بنابراین می‌توان صورت را به عنوان واحد تقریب زد) با این حال، اگرچه تقویت‌کننده رفتاری با دوقطب دارد، دو ثابت زمانی پیچیده‌تر از بیان فوق هستند، زیرا ظرفیت میلر حاوی وابستگی فرکانس پنهان است که در فرکانس‌های پایین اهمیتی ندارد، اما در فرکانس‌های بالا تأثیر قابل‌توجهی دارد؛ یعنی، با فرض اینکه حاصل R-C خروجی، C_L(R_o || R_L)، مربوط به یک فرکانس بسیار بالای قطب فرکانس پایین است، باید از شکل دقیق ظرفیت‌خازنی میلری استفاده شود، نه تقریب میلر. با توجه به مقاله در مورد اثر میلر، ظرفیت‌خازنی میلری داده شده است با

\begin{matrix} C_{M} & = C_{C} (1 - \frac{v_{ℓ}}{v_{i}}) \\ = C_{C} (1 - A_{v} \frac{R_{L}}{R_{L} + R_{o}} \frac{1 + j ω C_{C} R_{o} / A_{v}}{1 + j ω (C_{L} + C_{C}) (R_{o} ‖ R_{L})}) . \end{matrix}

(برای ظرفیت‌خازنی میلری مثبت، A_v منفی است) با جایگزینی این نتیجه به‌داخل عبارت بهره و جمع‌کردن جملات، بهره به صورت زیر بازنویسی می‌شود:

\frac{v_{ℓ}}{v_{a}} = A_{v} \frac{R_{i}}{R_{i} + R_{A}} \frac{R_{L}}{R_{L} + R_{o}} \frac{1 + j ω C_{C} R_{o} / A_{v}}{D_{ω}}

با D_ω داده شده توسط یک درجه‌دوم در ω، یعنی:

D_{ω}

= [1 + j ω (C_{L} + C_{C}) (R_{o} ‖ R_{L})]

\cdot [1 + j ω C_{i} (R_{A} ‖ R_{i})]

+ j ω C_{C} (R_{A} ‖ R_{i})

\cdot (1 - A_{v} \frac{R_{L}}{R_{L} + R_{O}})

+ (j ω)^{2} C_{C} C_{L} (R_{A} ‖ R_{i}) (R_{O} ‖ R_{L}) .

هر درجه‌دویی دو ضریب دارد و این عبارت اگر به صورت زیر بازنویسی شود ساده‌تر به نظر می‌رسد

D_{ω} = (1 + j ω τ_{1}) (1 + j ω τ_{2})

= 1 + j ω (τ_{1} + τ_{2})) + (j ω)^{2} τ_{1} τ_{2}

که در اینجا $τ_{1}$ و $τ_{2}$ ترکیبی از ظرفیت‌ها و مقاومت‌ها در فرمول D_ω هستند.^[۶] آنها با ثابت زمانی‌های دو قطب تقویت‌کننده مطابقت دارند. یکی یا آن دیگری طولانی‌ترین ثابت زمانی است. فرض کنید $τ_{1}$ طولانی‌ترین ثابت زمانی است که مربوط به پایین‌ترین قطب است و فرض کنید $τ_{1}$ >> $τ_{2}$ . (پاسخ پله خوب نیاز دارد $τ_{1}$ >> $τ_{2}$ . انتخاب C_C را در زیر ببینید)

در فرکانس‌های پایین نزدیک به پایین‌ترین قطب این تقویت‌کننده، معمولاً عبارت خطی در ω از جمله درجه‌دوم مهم‌تر است، بنابراین رفتار فرکانس پایین D_ω عبارت است از:

\begin{matrix} D_{ω} & = 1 + j ω [(C_{M} + C_{i}) (R_{A} ‖ R_{i}) + (C_{L} + C_{C}) (R_{o} ‖ R_{L})] \\ = 1 + j ω (τ_{1} + τ_{2}) \approx 1 + j ω τ_{1} \end{matrix}

که در حال حاضر C_M با استفاده از تقریب میلر دوباره تعریف می‌شود

C_{M} = C_{C} (1 - A_{v} \frac{R_{L}}{R_{L} + R_{o}}),

که به سادگی ظرفیت‌خازنی میلر قبلی است که در فرکانس‌های پایین ارزیابی شده است. بر این اساس $τ_{1}$ تعیین می‌شود، به شرط آنکه $τ_{1}$ >> $τ_{2}$ . از آنجا که C_M بزرگ است، ثابت زمانی $τ_{1}$ بسیار بزرگتر از مقدار اصلی C_i (R_A || R_i) است.^[۷]

در فرکانس‌های بالا عبارت درجه‌دوم مهم می‌شود. با فرض نتیجه فوق برای $τ_{1}$ معتبر باشد، ثابت زمانی دوم، موقعیت قطب فرکانس بالا، از عبارت درجه‌دوم در D_ω به‌صورتی یافت می‌شود که

τ_{2} = \frac{τ_{1} τ_{2}}{τ_{1}} \approx \frac{τ_{1} τ_{2}}{τ_{1} + τ_{2}} .

جایگزینی در این عبارت ضریب درجه‌دوم مربوط به حاصل‌ضرب $τ_{1} τ_{2}$ همراه با تخمینی برای $τ_{1}$ ، تخمینی برای موقعیت قطب دوم یافت می‌شود:

\begin{matrix} τ_{2} & = \frac{(C_{C} C_{L} + C_{L} C_{i} + C_{i} C_{C}) (R_{A} ‖ R_{i}) (R_{O} ‖ R_{L})}{(C_{M} + C_{i}) (R_{A} ‖ R_{i}) + (C_{L} + C_{C}) (R_{o} ‖ R_{L})} \\ \approx \frac{C_{C} C_{L} + C_{L} C_{i} + C_{i} C_{C}}{C_{M}} (R_{O} ‖ R_{L}) \end{matrix}

و چون C_M بزرگ است، به نظر می‌رسد $τ_{2}$ در اندازه از مقدار اصلی خود C_L(R_o || R_L) کاهش می‌یابد؛ یعنی قطب بالاتر به دلیل C_C هنوز از نظر فرکانس بالاتر برده است.^[۸]

به‌طور خلاصه، واردکردن خازن C_C قطب پایین را پایین‌تر و قطب بالا را بالاتر برد، بنابراین اصطلاح دوپاره‌سازی قطب توصیف خوبی به نظر می‌رسد.

انتخاب C_C

یک انتخاب خوب برای C_C چه مقداری است؟ برای استفاده عمومی، طراحی سنتی (اغلب به عنوان جبران‌سازی قطب‌غالب یا تک‌قطبی نامیده می‌شود) نیاز به کاهش بهره تقویت‌کننده در ۲۰ دسی‌بل در دهه از فرکانس گوشه تا بهره ۰ دسی بل، یا حتی کمتر دارد.^[۹]^[۱۰] با این طراحی، تقویت‌کننده پایدار است و حتی به عنوان یک بافر ولتاژ با بهره واحد، پاسخ پله تقریباً بهینه دارد. یک فنّ تهاجمی‌تر، جبران دوقطب است.^[۱۱]^[۱۲]

نحوه موقعیت f₂ برای به دست آوردن طرح در شکل ۳ نشان داده شده است. در پایین‌ترین قطب f ₁، نمودار بهره بُود شیب را می‌شکند تا در ۲۰ دسی بل/دهه سقوط کند. هدف نگه‌داشتن شیب ۲۰ دسی بل در دهه تا صفر دسی‌بل است، و نسبت افت مورد نظر بهره (برحسب دسی‌بل) $20 \log_{10} A v$ به تغییر در فرکانس مورد نیاز (در مقیاس log فرکانس^[۱۳]) از $(\log_{10} f_{2} - \log_{10} f_{1}) = \log_{10} (f_{2} / f_{1})$ شیب تِکه بین f₁ و f₂ است:

شیب در هر دهه فرکانس

= 20 \frac{l o g_{10} (A_{v})}{l o g_{10} (f_{2} / f_{1})},

که ۲۰ دسی‌بل بر دهه استبه شرط اینکه f₂ = A_v f₁. اگر f₂ به این بزرگی نباشد، شکست دوم در نمودار بود که در قطب دوم رخ می‌دهد، نمودار را قبل از افت بهره به ۰ دسی‌بل قطع می‌کند. با پیامد پایداری کمتر و پاسخ پله نزول‌یافته.

شکل ۳ نشان می‌دهد که برای به دست آوردن وابستگی بهره صحیح به فرکانس، قطب دوم حداقل یک ضریب A_v در فرکانسی بالاتر از قطب اول است. بهره توسط تقسیم‌کننده‌های ولتاژ در ورودی و خروجی تقویت‌کننده کمی کاهش می‌یابد، بنابراین با اصلاحات A_v برای تقسیم‌کننده‌های ولتاژ در ورودی و خروجی، شرایط نسبت قطب برای پاسخ پله خوب به این صورت می‌شود:

\frac{τ_{1}}{τ_{2}} \approx A_{v} \frac{R_{i}}{R_{i} + R_{A}} \cdot \frac{R_{L}}{R_{L} + R_{o}}

با استفاده از تقریب‌های ثابت زمانی که در بالا ایجاد شده است،

\frac{τ_{1}}{τ_{2}} \approx \frac{(τ_{1} + τ_{2})^{2}}{τ_{1} τ_{2}} \approx A_{v} \frac{R_{i}}{R_{i} + R_{A}} \cdot \frac{R_{L}}{R_{L} + R_{o}},

یا

\frac{[(C_{M} + C_{i}) (R_{A} ‖ R_{i}) + (C_{L} + C_{C}) (R_{o} ‖ R_{L})]^{2}}{(C_{C} C_{L} + C_{L} C_{i} + C_{i} C_{C}) (R_{A} ‖ R_{i}) (R_{O} ‖ R_{L})}

\cdot = A_{v} \frac{R_{i}}{R_{i} + R_{A}} \cdot \frac{R_{L}}{R_{L} + R_{o}},

که یک معادله درجه دوم برای تعیین مقدار مناسب برای C_C ارائه می‌کند. شکل ۴ نمونه‌ای را با استفاده از این معادله نشان می‌دهد. در مقادیر کم بهره، این تقویت‌کننده مثالی، شرایط نسبت قطب را بدون جبران‌سازی برآورده می‌کند (یعنی در شکل ۴، خازن جبران‌سازی C_C در بهره کم کوچک است)، اما با افزایش بهره، ظرفیت‌خازنی جبران‌سازی به سرعت لازم می‌شود (یعنی در شکل ۴ خازن جبران‌سازی C_C به سرعت با بهره افزایش می‌یابد) زیرا نسبت قطب لازم با بهره افزایش می‌یابد. برای بهره هنوز بزرگتر، C_C لازم با افزایش بهره کاهش می‌یابد، زیرا تقویت میلر C_C، که با بهره افزایش می‌یابد (به معادله میلر مراجعه کنید)، مقدار کمتری را برای C_C اجازه می‌دهد.

برای ارائه حاشیه ایمنی بیشتر برای عدم قطعیت‌های طراحی، اغلب A_v به دو یا سه برابر A_v در سمت راست این معادله افزایش می‌یابد.^[۱۴] سانسن^[۴] یا هوایجینگ^[۱۰] و مقاله در مورد پاسخ پله را ببینید.

نرخ چرخش

موارد فوق یک تحلیل سیگنال کوچک است. با این حال، هنگامی که از سیگنال‌های بزرگ استفاده می‌شود، نیاز به شارژ و تخلیه خازن جبران‌سازی بر نرخ چرخش تقویت‌کننده تأثیر منفی می‌گذارد. به ویژه، پاسخ به سیگنال رَمپ ورودی به دلیل نیاز به شارژ C_C محدود می‌شود.

جستارهای وابسته

مراجع و یادداشت‌ها

الگو:چپ‌چین الگو:پانویس الگو:پایان چپ‌چین

پیوند به بیرون

ترسیم‌های بود در ویکی‌کتاب تئوری مدار
ترسیم‌های بود در ویکی‌کتاب سیستم‌های کنترل

↑ That is, the rise time is selected to be the fastest possible consistent with low overshoot and ringing.
↑ الگو:Cite book
↑ الگو:Cite book
↑ ^۴٫۰ ^۴٫۱ الگو:Cite book
↑ Although this example appears very specific, the associated mathematical analysis is very much used in circuit design.
↑ The sum of the time constants is the coefficient of the term linear in jω and the product of the time constants is the coefficient of the quadratic term in (jω)².
↑ The expression for $τ_{1}$ differs a little from (C_M+C_i) (R_A || R_i) as found initially for f₁, but the difference is minor assuming the load capacitance is not so large that it controls the low frequency response instead of the Miller capacitance.
↑ As an aside, the higher the high-frequency pole is made in frequency, the more likely it becomes for a real amplifier that other poles (not considered in this analysis) play a part.
↑ الگو:Cite book
↑ ^۱۰٫۰ ^۱۰٫۱ الگو:Cite book
↑ Feucht, Dennis: Two-pole compensation
↑ الگو:Cite book
↑ That is, the frequency is plotted in powers of ten, as 1, 10, 10² etc.
↑ A factor of two results in the maximally flat or Butterworth design for a two-pole amplifier. However, real amplifiers have more than two poles, and a factor greater than two often is necessary.

[1] That is, the rise time is selected to be the fastest possible consistent with low overshoot and ringing.

[Toumazou2-2] الگو:Cite book

[Thompson2-3] الگو:Cite book

[Sansen2-4] ۴٫۰ ^۴٫۱ الگو:Cite book

[5] Although this example appears very specific, the associated mathematical analysis is very much used in circuit design.

[6] The sum of the time constants is the coefficient of the term linear in jω and the product of the time constants is the coefficient of the quadratic term in (jω)².

[7] The expression for $τ_{1}$ differs a little from (C_M+C_i) (R_A || R_i) as found initially for f₁, but the difference is minor assuming the load capacitance is not so large that it controls the low frequency response instead of the Miller capacitance.

[8] As an aside, the higher the high-frequency pole is made in frequency, the more likely it becomes for a real amplifier that other poles (not considered in this analysis) play a part.

[Sedra2-9] الگو:Cite book

[Huijsing2-10] ۱۰٫۰ ^۱۰٫۱ الگو:Cite book

[11] Feucht, Dennis: Two-pole compensation

[Self2-12] الگو:Cite book

[13] That is, the frequency is plotted in powers of ten, as 1, 10, 10² etc.

[14] A factor of two results in the maximally flat or Butterworth design for a two-pole amplifier. However, real amplifiers have more than two poles, and a factor greater than two often is necessary.

[۱]

[۲]

[۳]

[۴]

[۵]

[۶]

[۷]

[۸]

[۹]

[۱۰]

[۱۱]

[۱۲]

[۱۳]

[۱۴]

دوپاره‌سازی قطب

فهرست

نمونه‌ای از دوپاره‌سازی قطب

انتخاب C_C

نرخ چرخش

جستارهای وابسته

مراجع و یادداشت‌ها

پیوند به بیرون

منوی ناوبری

دوپاره‌سازی قطب

نمونه‌ای از دوپاره‌سازی قطب

انتخاب CC

نرخ چرخش

جستارهای وابسته

مراجع و یادداشت‌ها

پیوند به بیرون

منوی ناوبری

جستجو

انتخاب C_C