الگوریتم کاراتسوبا

آناتولی کاراتسوبا

الگوریتم کاراتسوبا یک الگوریتم سریع برای ضرب اعداد است. الگوریتم کاراتسوبا اولین الگوریتمی است که به صورت مجانبی سریع است. این الگوریتم برای اولین‌بار توسط آناتولی کاراتسوبا در سال ۱۹۶۲ ارائه شد. این الگوریتم با استفاده از روش تقسیم و حل تعداد عملیات ضرب لازم برای ضرب دو عدد n رقمی را کاهش می‌دهد. الگو:سخ در عملیات ضرب معمولی که در دبیرستان آموزش داده می‌شود، به تعداد n^۲ عملیات ضرب لازم است. این الگوریتم تعداد عملیات ضرب را به 3n^log3_۲ می‌رساند. الگو:سخ ۳ سال بعد ارائه این الگوریتم توسط کاراتسوبا، الگوریتم Toom-Cook algorithm ارائه شد که حالت کلی‌تر و سریع‌تر همین الگوریتم است. علاوه بر این در سال ۱۹۷۱ الگوریتم Schönhage–Strassen algorithm ارائه شد که برای اعداد بزرگ از الگوریتم کاراتسوبا سریع‌تر است و بهتر عمل می‌کند.

تاریخچه

در سال ۱۹۵۲ آندره کولوموگوروف ادعا کرد که الگوریتم ضرب کلاسیک از نظر پیچیدگی زمانی بهینه‌است و هر الگوریتم دیگری که برای ضرب دو عدد ارائه شود، حداقل $\mathrm{\Omega }(n^2)$ عملیات نیاز دارد. سپس در پاییز ۸ سال بعد یعنی سال ۱۹۶۰، در دانشکده مکانیک و ریاضی داشگاه مسکو، سمیناری برگزار و این ادعا را در زمینه پیچیدگی محاسباتی مطرح کرد. الگو:سخ در کمتر از یک هفته، کاراتسوبا که در آن زمان ۲۳ ساله بود، الگوریتمی ارائه کرد که به $\mathrm{\Theta }(n^{{\log }_{2}3})$ عملیات نیاز داشت و به این ترتیب فرضیه کولوموگوروف را رد کرد. او فرضیه خود را بعد از سمینار بعدی با کولوموگوروف در میان گذاشت. کولوموگوروف از این موضوع بسیار آشفته شد، به این خاطر که این الگوریتم به‌طور کامل نظریهٔ او را رد می‌کرد. الگو:سخ دو سال بعد کولوموگوروف این الگوریتم به صورت مقاله‌ای کوتاه درآورد و نام کاراتسوبا را در آن قرار داد. نکته جالب توجه آن است که کاراتسوبا پس از انتشار مقاله، از آن باخبر شد. الگو:سخ بعد از انتشار این الگوریتم، روشی که کاراتسوبا به کار برد به نام روش تقسیم و حل (divide and conquer) نامیده شد. الگو:سخ پیدایش روش تقسیم و حل، نقطه شروع نظریه محاسبات سریع بود. پژوهشگرانی مانند توم، کوک و اشتغاسن تلاش‌های زیادی در این زمینه انجام دادند، که الگوریتم اشتغاسن بهترین الگوریتم از منظر زمان اجرا در این زمینه‌است. الگو:سخ روش تقسیم و حل کاراتسوبا، از پایه‌ای‌ترین روش‌ها در این زمینه‌است. صدها الگوریتم بر پایهٔ این الگوریتم به وجود آمده‌اند که مهمترین و مشهورترین آنها، الگوریتم ضرب بر پایه تبدیل سریع فوریه است.

الگوریتم

حالت خاص

الگوریتم به روش تقسیم و حل عمل می‌کند. به این معنا که ابتدا هر کدام از اعداد را به قسمت‌های کوچکتر تقسیم کرده و سپس به صورت بازگشتی، روی آن‌ها ضرب را انجام می‌دهد. الگو:سخ ابتدا حالت ساده‌ای را در نظر می‌گیریم. این حالت به راحتی قابل تعمیم به روش کلی است. الگو:سخ فرض کنید عدد اول X و عدد دوم Y است. هر دو عدد صحیح و در مبنای دو و دارای n رقم که n توانی از ۲ است. در ابتدا دو عدد مطابق شکل به دو قسمت تقسیم می‌شوند. X_۱ قسمت پرارزش و X_۰ قسمت کم‌ارزش است. به صورت مشابه، برای Y هم به همین صورت است. پس داریم:

تقسیم عددها به دو قسمت

الگو:چپ‌چین X = X_۱ ۲^(n/2) + X_۰ الگو:سخ Y= Y_۱ ۲^(n/2) + Y_۰ الگو:سخ الگو:پایان چپ‌چین به این ترتیب ضرب XY به صورت زیر در می‌آید: الگو:سخ الگو:سخ الگو:چپ‌چین XY = (X_۱ ۲^(n/2) + X_۰) (Y_۱ ۲^(n/2) + Y_۰) الگو:سخ XY = x_۱y_۱۲ⁿ + (x_۱y_۰ + x_۰y_۱)۲^(n/2) + x_۰y_۰ الگو:پایان چپ‌چین

در مبنای ۲، ضرب یک عدد در توانی از ۲، به صورت عملیات شیفت در کامپیوتر به راحتی انجام می‌شود. عملیات شیفت و جمع، در مقابل عملیات ضرب، زمان اجرای بسیار کمی دارند. به همین خاطر، زمان اجرای آن را از (1)O در نظر می‌گیرند. حال مسئله به ۴ زیرمسئله با اندازهٔ نصف مسئله قبلی تبدیل شده‌است؛ بنابراین می‌توان این ۴ مسئله را به روش بازگشتی حل و در زمان خطی، عبارت کلی را محاسبه کرد. پیچیدگی زمانی رابطه بالا به صورت زیر است: الگو:سخ الگو:سخ الگو:چپ‌چین T(n) = 4T(n/2) + O(n)

الگو:پایان چپ‌چین الگو:سخ که (T(n زمان اجرای برای ضرب دو عدد n بیتی است. زمان اجرای آن از (O(n است. الگو:سخ پس هنوز بهبودی صورت نیافته‌است. الگو:سخ با یک راه حل ساده می‌توان تعداد ضرب‌های انجام شده را از ۴ به ۳ رساند. الگو:سخ فرض کنید: الگو:چپ‌چین x_۲ = x_۱ + x_۰ الگو:سخ y_۲ = y_۱ + y_۰ الگو:پایان چپ‌چین با داشتن x_۲ و y_۲ می‌توان تنها با استفاده از ۳ جمله این ضرب را انجام داد. به این ترتیب که به جای جملهٔ (x_۱y_۰ + x_۰y_۱) از(x_۲y_۲ – x_۰y_۰ - x_۱y_۱) استفاده کنیم. الگو:سخ به این ترتیب برای انجام مرحلهٔ بازگشتی تنها به ۳ جمله نیاز است: الگو:چپ‌چین

• x_۰y_۰
• x_۱y_۱
• x_۲y_۲

الگو:پایان چپ‌چین پس زمان اجرا به صورت زیر در می‌آید: الگو:چپ‌چین T(n) = 3T(n/2) + O(n) الگو:سخ-->T(n) = O(n^log3_۲) الگو:پایان چپ‌چین با این ترفند ساده به راحتی زمان اجرا بهبود یافت.

تحلیل دقیق‌تر زمان اجرا

با رسم درخت بازگشت این الگوریتم، شهود بهتری نسبت به آن در این حالت خاص، بدست می‌آید. درخت بازگشت را در شکل زیر در نظر بگیرید.

درخت بازگشت در الگوریتم کاراتسوبا

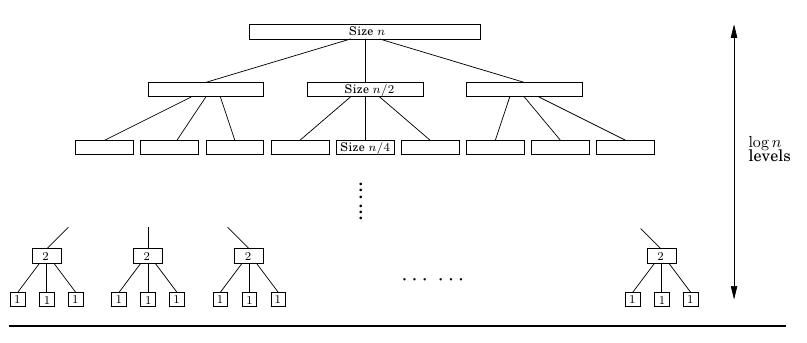
در هر عمق از این درخت مسئله به ۳ مسئله با اندازه نصف تبدیل می‌شود. در عمق (log_۲(n به زیر مسئله‌ای با اندازه یک تبدیل می‌شود و روند بازگشتی متوقف می‌شود؛ بنابراین ارتفاع درخت برابر (log_۲(n است. الگو:سخ اگر عمقی مانند k را در نظر گرفته شود، ۳^k زیر مسئله با اندازه n /2^k وجود دارد. برای هر کدام از این زیر مسئله‌ها، کافی است عملیاتی با هزینهٔ خطی بپردازیم. این عملیات شامل جمع کردن زیرمسئله‌ها و تقسیم‌کردن هر کدام به زیرمسئله‌هایی کوچکتر است؛ بنابراین، در عمق kام هزینه‌ای معادل زیر پرداخت می‌کنیم: الگو:چپ‌چین ۳^kO(n/2^k) = (۳/۲)^k O(n)

الگو:پایان وسط‌چین حال اگر همهٔ هزینه‌ها را در عمق‌های مختلف جمع کنیم، هزینه کل برابر (O(n^log3_۲ خواهد شد. در حالیکه اگر در هر مرحله به ۴ زیرمسئله تقسیم می‌شد و از این نکته استفاده نمی‌شد، زمان اجرا برابر (O(n^۲ می‌شود. به کمک قضیهٔ اصلی نیز می‌توان زمان اجرا را محاسبه کرد که به همین نتیجه ختم خواهد شد.

حالت کلی

در این قسمت حالت کلی الگوریتم کاراتسوبا توضیح داده می‌شود. الگو:سخ فرض کنید X و Y دو عدد n رقمی در مبنای B هستند. به ازای هر m کوچکتر از n می‌توان این دو عدد را به صورت زیر نوشت: الگو:چپ‌چین XY = (x_۱B^m + x_۰) (y_۱B^m + y_۰) الگو:سخ XY = x_۱y_۱B^2m + (x_۱y_۰ + x_۰y_۱)B^m + x_۰y_۰ الگو:سخ الگو:پایان چپ‌چین

مشابه ایده‌ای که در بالا گفته شد می‌توان این ۴ ضرب را تنها با ۳ ضرب و چند عملیات جمع اضافه انجام داد. کافی است به جای (x_۱y_۰ + x_۰y_۱) از x_۱+x_۰) (y_۱+y_۰) - x_۰y_۰ - x_۱y_۱) استفاده کنیم؛ بنابراین: الگو:چپ‌چین XY = x_۱y_۱B^2m + ((x_۱+x_۰)(y_۱+y_۰) - (x_۰y_۰) - (x_۱y_۱)B^m + x_۰y_۰ الگو:پایان چپ‌چین

مثال

فرض کنید می‌خواهیم حاصل‌ضرب دو عدد ۱۲۳۴ و ۵۶۷۸ را بدست آوریم. دو عدد دهدهی هستند پس B = ۱۰ است. m را نیز ۲ انتخاب می‌کنیم. الگو:چپ‌چین

۱۲ ۳۴ = ۱۲ × ۱۰^۲ + ۳۴

۵۶ ۷۸ = ۵۶ × ۱۰^۲ + ۷۸

x_۱y_۱ = ۱۲ × ۵۶ = ۶۷۲

x_۰y_۰ = ۳۴ × ۷۸ = ۲۶۵۲

(x_۱ + x_۰)(y_۱ + y_۰) = (۱۲ + ۳۴)(۵۶ + ۷۸) = ۲۸۴۰

result = 672 × ۱۰۰۰۰ + ۲۸۴۰ × ۱۰۰ + ۲۶۵۲ = ۷۰۰۶۶۵۲.

پیاده‌سازی

شبه‌کد الگوریتم به صورت زیر است: الگو:چپ‌چین

 1 Algorithm karatsuba_multiplication(X,Y)
 2 Input: X and Y two binary number)
 3 Output: product of X and Y
 4 begin
 5 if n = 1: return xy
 6 x۱ = X>> n/2
 7 x۰ = X mod 2 n/2
 8 y۱ = Y>> n/2
 9 y۰ = Y mod 2 n/2
 10 x۲ = x۱ + x۰
 11 y۲ = y۱ + y۰
 12 R۱ = multiply(x۱ , y۱)
 13 R۲ = multiply(x۰ , y۰)
 14 R۳ = multiply(x۲ , y۲)
 15 return R۱ × ۲n + (R۳ − R۱ − R۲) × ۲n/2 + R۲
 16 end

الگو:پایان چپ‌چین پیاده‌سازی الگوریتم با استفاده از جاوا: الگو:چپ‌چین

import java.math.BigInteger;
import java.util.Random;

class Karatsuba {
    private final static BigInteger ZERO = new BigInteger("0");

    public static BigInteger karatsuba(BigInteger x, BigInteger y) {

        // cutoff to brute force
        int N = Math.max(x.bitLength(), y.bitLength());
        if (N <= 2000) return x.multiply(y);                // optimize this parameter

        // number of bits divided by 2, rounded up
        N = (N / 2) + (N % 2);

        // x = a + 2^N b,   y = c + 2^N d
        BigInteger b = x.shiftRight(N);
        BigInteger a = x.subtract(b.shiftLeft(N));
        BigInteger d = y.shiftRight(N);
        BigInteger c = y.subtract(d.shiftLeft(N));

        // compute sub-expressions
        BigInteger ac    = karatsuba(a, c);
        BigInteger bd    = karatsuba(b, d);
        BigInteger abcd  = karatsuba(a.add(b), c.add(d));

        return ac.add(abcd.subtract(ac).subtract(bd).shiftLeft(N)).add(bd.shiftLeft(2*N));
   }

    public static void main(String[] args) {
        long start, stop, elapsed;
        Random random = new Random();
        int N = Integer.parseInt(args[0]);
        BigInteger a = new BigInteger(N, random);
        BigInteger b = new BigInteger(N, random);

        start = System.currentTimeMillis();
        BigInteger c = karatsuba(a, b);
        stop = System.currentTimeMillis();
        System.out.println(stop - start);

        start = System.currentTimeMillis();
        BigInteger d = a.multiply(b);
        stop = System.currentTimeMillis();
        System.out.println(stop - start);

        System.out.println((c.equals(d)));
   }
}

الگو:پایان چپ‌چین پیاده‌سازی الگوریتم با استفاده از پایتون: الگو:چپ‌چین

_CUTOFF = ۱۵۳۶;

def multiply(x, y):
    if x.bit_length() <= _CUTOFF or y.bit_length() <= _CUTOFF:  # Base case
        return x * y;

    else:
        n = max(x.bit_length(), y.bit_length())
        half = (n + 32) / 64 * 32
        mask = (۱ <<half) - 1
        xlow = x & mask
        ylow = y & mask
        xhigh = x>> half
        yhigh = y>> half

        a = multiply(xhigh, yhigh)
        b = multiply(xlow + xhigh, ylow + yhigh)
        c = multiply(xlow, ylow)
        d = b - a - c
        return (((a <<half) + d) <<half) + c

الگوریتم کاراتسوبا در عمل

همان طور که دیدیم الگوریتم به صورت بازگشتی مسئله را به زیر مسئله‌هایی با اندازه نصف مسئله اولیه تبدیل کرده و این کار را تا تبدیل آن به زیر مسئله‌ای با اندازه یک ادامه می‌دهد. دلیل این کار این است که فرض شده‌است عمل ضرب دو عدد یک رقمی در(1)O انجام می‌گیرد. الگو:سخ

در حالیکه در پردازنده‌های امروزی این گونه نیست بسیاری از پردازنده‌ها ضرب ۱۶ بیتی یا ۳۲ بیتی را در یک عملیات انجام می‌دهند. یعنی در معماری این پردازنده‌ها واحد ضرب‌کننده ۳۲ بیتی یا ۱۶ بیتی وجود دارد. به همین خاطر در عمل لازم نیست که به صورت بازگشتی با زیر مسئله‌ای با اندازه ۱ پایین برویم. با داشتن آگاهی نسبت به معماری پردازنده، می‌توان B و m را به گونه‌ای انتخاب کرد که کارایی و زمان اجرای بهتری از الگوریتم بدست آید.

جستارهای وابسته

• روش تقسیم و حل
• ضرب
• تبدیل سریع فوریه

پیوند به بیرون

• الگوریتم کاراتسوبا یه همراه اپلت جاوا
• الگوریتم به همراه مثالالگو:پیوند مرده
• توضیحات الگوریتم به همراه کد و مقایسه آن با روش عادی ضرب
• کد الگوریتم به زبان ++C و مقایسه آن با روش عادی ضرب