تولید هارمونیک مرتبه بالا

الگو:ویکی سازی

هارمونیک‌ها به‌وسیلهٔ بارهای غیرخطی تولید می‌شوند. وقتی که یک ولتاژ با موج سینوسی به این نوع بارها اعمال می‌شود، جریانی را که مصرف می‌کنند، شکل موج غیر سینوسی است.

تولید هارمونیک مرتبه بالا در گازهای اتمی برای دهه‌ها مورد مطالعه قرار گرفته است و اساس علم آتوثانیه را تشکیل داده است. با این حال، مشاهده هارمونیک‌های مرتبه بالا از کریستال‌های توده‌ای اخیراً در سال ۲۰۱۰ گزارش شده است.

تولید با هارمونیک بالا (HHG) یک فرایند غیر خطی است که طی آن یک هدف (گاز، پلاسما، نمونه جامد یا مایع) توسط یک پالس لیزر شدید روشن می‌شود. در چنین شرایطی، نمونه هارمونیک بالای پرتو تولید (بالاتر از هارمونیک پنجم) را منتشر می‌کند. به دلیل ماهیت منسجم فرایند، تولید با هارمونیک بالا پیش نیاز فیزیک آتوثانیه است.

تولید هارمونیک اختلالی

تولید هارمونیک اختلالی فرآیندی است که در آن از نور لیزر با فرکانس ω و انرژی فوتون ħω می‌توان برای تولید فرکانس‌های جدید نور استفاده کرد. در این زمینه، فرکانس‌های تولیدشده مضرب صحیح nω فرکانس نور اصلی هستند. این فرایند اولین بار در سال ۱۹۶۱ توسط فرانکن و همکاران با استفاده از لیزر یاقوتی با کوارتز بلورین به عنوان محیط غیرخطی کشف شد.

تولید هارمونیک در جامدات دیالکتریک به خوبی درک شده‌است و به‌طور گسترده در فیزیک لیزر مدرن استفاده می‌شود. در سال ۱۹۶۷ نیو و همکاران، اولین نسل سوم هارمونیک را در گاز مشاهده کردند.

در گازهای تک اتمی تولید با هارمونیک مرتبه بالا تنها به دلایل تقارن امکان‌پذیر است. همچنین، تولید هارمونیک در رژیم اختلالی (میدان ضعیف) با کاهش سریع راندمان با افزایش نظم هارمونیک مشخص می‌شود. این رفتار را می‌توان با در نظر گرفتن اتمی که n فوتون را جذب می‌کند و سپس یک فوتون با انرژی بالا را ساطع می‌کند، درک کرد. بر این اساس، احتمال جذب n فوتون با افزایش n کاهش می‌یابد که کاهش سریع شدت هارمونیک اولیه را توجیه می‌کند [۴].

ایجاد

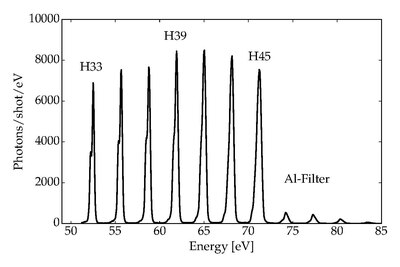
اولین نسل هارمونیک بالا در سال ۱۹۷۷ در تعامل پالس‌های لیزر CO₂ شدید با پلاسمای تولیدشده از اهداف جامد مشاهده شد. HHG در گازها که امروزه کاربرد بسیار گسترده‌تری دارد، اولین بار توسط مک فرسون و همکارانش در سال ۱۹۸۷ مشاهده شد و بعداً توسط Ferray و همکارانش مشاهده می‌شود. همچنین، در سال ۱۹۸۸ با نتایج شگفت‌انگیزی مشخص شد که هارمونیک‌های مرتبه بالا در کاهش شدت در مرتبه‌های پایین یافت می‌گردد اما پس از آن مشاهده شد که یک فلات را تشکیل می‌دهند که شدت هارمونیک‌ها تقریباً در بسیاری از مرتبه‌ها ثابت می‌ماند. هارمونیک‌های فلات که صدها eV را در بر میگیرد، اندازه‌گیری شدهاست که به رژیم اشعه ایکس نرم گسترش می‌یابد. این فلات به‌طور ناگهانی به موقعیتی به نام برش هارمونیک بالا ختم می‌شود. شکل ۳ طیف یک منبع HHG نئونی که توسط لیزر Ti-Sapphire هدایت می‌شود را به تصویر می‌کشد.

ویژگی‌ها

هارمونیک مرتبه بالا تعدادی ویژگی جالب دارد. آنها یک منبع قابل تنظیم از XUV/اشعه ایکس نرم هستند که با لیزر محرک هماهنگ شده و با همان نرخ تولید می‌شوند. در این زمینه، برش هارمونیک به صورت خطی با افزایش شدت لیزر تا شدت اشباع که در آن تولید هارمونیک متوقف می‌شود، تغییر می‌کند. همچنین، شدت اشباع را می‌توان با تغییر گونه‌های اتمی به گازهای نجیب سبک‌تر افزایش داد، اما این گازها بازده تبدیل کمتری دارند؛ بنابراین بسته به انرژی‌های فوتون مورد نیاز، تعادلی وجود دارد.

تولید هارمونیک مرتبه بالا به شدت به میدان لیزر محرک بستگی دارد و در نتیجه هارمونیک‌ها خواص انسجام زمانی و مکانی مشابهی دارند. همچنین، هارمونیک مرتبه بالا اغلب با مدت زمان پالس کوتاه‌تر از لیزر محرک تولید می‌شوند. این به دلیل غیر خطی بودن فرایند تولید، تطبیق فاز و یونیزاسیون است. اغلب هارمونیک‌ها فقط در یک پنجره زمانی بسیار کوچک تولید می‌شوند که شرایط تطابق فاز برآورده شود. تخلیه محیط مولد به دلیل یونیزاسیون به این معنی است که تولید هارمونیک عمدتاً به لبه جلویی پالس محرک محدود می‌شود.

علاوه‌براین، هارمونیک‌های مرتبه بالا به صورت خطی با لیزر محرک ساطع می‌شوند و می‌توانند محدودیت زاویه‌ای بسیار کوچکی داشته باشند؛ گاهی اوقات با واگرایی کمتری نسبت به میدان بنیادی و نزدیک پروفیل‌های پرتو گاوسی [۴].

رویکرد جوبان

حداکثر انرژی فوتون قابل تولید با تولید هارمونیک بالا توسط برش فلات هارمونیک بدست می‌آید. این را می‌توان به صورت کلاسیک با بررسی حداکثر انرژی که الکترون یونیزه می‌تواند در میدان الکتریکی لیزر بدست آورد، محاسبه کرد.

انرژی قطع شده توسط معادله زیر بدست میآید:

ponderomotive

E_max=I_p+3.17 U_p

که در آن U _p انرژی محرک میدان لیزر و I _p پتانسیل یونیزاسیون است.

این استخراج انرژی از یک محاسبه نیمه کلاسیک بدست می‌آید. الکترون در ابتدا به صورت مکانیکی کوانتومی به عنوان تونل از اتم مادر یونیزه می‌شود، اما سپس دینامیک بعدی آن به صورت کلاسیک بررسی می‌شود. فرض بر این است که الکترون با سرعت اولیه صفر در خلأ متولد می‌شود و متعاقباً توسط میدان الکتریکی پرتو لیزر شتاب میگیرد. شکل ۴ تصویر مدل سه مرحلهای نیمه کلاسیک HHG را به تصویر می‌کشد.

Illustration of the semi-classical three-step model of HHG — مدل سه مرحله ای

پس از یونیزاسیون، الکترون با تغییر میدان الکتریکی جهت خود را معکوس کرده و به سمت هسته اصلی شتاب خواهد گرفت. پس از بازگشت به هسته والد، میتواند تشعشعات برومزاششترلانگ مانند را در طی فرایند نوترکیبی با اتم در حین بازگشت به حالت اولیه خود منتشر کند. این توصیف به عنوان مدل برخوردی تولید هارمونیک بالا شناخته شده‌است.

bremsstrahlung

انرژی برگشتی الکترون (منحنی آبی کامل) و زمان گشت و گذار (منحنی نقطه چین آبی)، به عنوان تابعی از زمان بازگشت

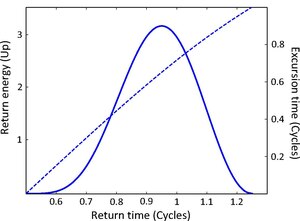
از آنجایی که فرکانس تابش ساطع شده هم به انرژی جنبشی و هم به پتانسیل یونیزاسیون بستگی دارد، فرکانس‌های مختلف در زمان‌های نوترکیبی مختلف گسیل می‌شوند (یعنی پالس ساطعشده به صدا در می‌آید). علاوه‌براین، برای هر فرکانس، دو زمان نوترکیب متناظر وجود دارد. به این دو مسیر به عنوان مسیر کوتاه (که ابتدا منتشر می‌شود) و مسیر طولانی اشاره می‌شود.

برخی از محدودیت‌های جالب در فرایند HHG که توسط این مدل توضیح داده شده‌اند، نشان می‌دهند که HHG تنها زمانی رخ می‌دهد که میدان لیزر محرک به صورت خطی قطبی شده باشد. بیضی بودن در پرتو لیزر باعث می‌شود که الکترون برگشتی هسته اصلی را از دست بدهد. به عبارتی دیگر، از نظر مکانیک کوانتوم، همپوشانی بسته موج الکترون برگشتی با بسته موج هسته‌ای کاهش می‌یابد. این موضوع به صورت تجربی مشاهده شده‌است؛ جایی که شدت هارمونیک‌ها با افزایش بیضی به سرعت کاهش می‌یابد.

اثر دیگری که شدت لیزر محرک را محدود می‌کند، نیروی لورنتس است. در شدت‌های بالاتر از Wcm^-2 10¹⁶، جزء مغناطیسی پالس لیزر که در اپتیک میدان ضعیف نادیده گرفته می‌شود، می‌تواند آنقدر قوی شود که الکترون برگشتی را منحرف کند. این امر باعث می‌شود که هسته مادر را از دست بدهد و در نتیجه از HHG جلوگیری کند.

تطبیق فاز

همانند هر فرایند غیرخطی، تطبیق فاز نقش مهمی در تولید هارمونیک مرتبه بالا در فاز گاز دارد. در هندسه با تمرکز آزاد، چهار علت عدم تطابق بردار موج عبارتند از: پراکندگی خنثی، پراکندگی پلاسما، فاز گوی و فاز دوقطبی.

پراکندگی خنثی توسط اتمها ایجاد می‌شود، در حالیکه پراکندگی پلاسما به دلیل یون‌ها است و این دو دارای علائم متضاد هستند. فاز Gouy نیز به دلیل پرش فاز جبهه موج نزدیک به کانون است و در طول آن تغییر می‌کند. در نهایت فاز دوقطبی از پاسخ اتمی در فرایند HHG بوجود می‌آید. هنگام استفاده از هندسه جت گاز[۲]، شرایط بهینه برای تولید هارمونیک‌های مرتبه بالا ساطع‌شده از مسیرهای کوتاه زمانی حاصل می‌شود که گاز مولد بعد از فوکوس قرار گیرد، در حالیکه تولید هارمونیک‌های مرتبه بالا از مسیر طولانی را می‌توان در خارج از محور زمانی که گاز مولد قبل از فوکوس قرار دارد بدست آورد.

علاوه‌براین، اجرای هندسه با فوکوس سست برای میدان محرک، تعداد بیشتری از تابش‌کنندگان و فوتون‌ها را قادر می‌سازد تا به فرایند تولید کمک کنند و در نتیجه، تسلیم هارمونیک را افزایش دهند. هنگام استفاده از هندسه جت گاز، تمرکز لیزر بر روی دیسک ماخ[۳] می‌تواند کارایی تولید هارمونیک را افزایش دهد.

به‌طور کلی، در ناحیه طیفی اشعه ایکس، مواد دارای ضریب شکست بسیار نزدیک به ۱ هستند. برای متعادل کردن عدم تطابق فاز، K=K_q - qK_L∆ باید چنین پارامترهایی را در فضای با ابعاد بالا پیدا کرد که به‌طور مؤثر ضریب شکست ترکیبی در طول موج لیزر محرک را نزدیک به ۱ کند.

برای دستیابی به سطوح شدتی که می‌تواند پتانسیل اتصال اتم را مخدوش کند، لازم است پرتو لیزر محرک، متمرکز شود. این شرایط پراکندگی را معرفی می‌کند که بسته به هندسه خاص (مانند انتشار موج صفحه، تمرکز آزاد، موجبر هسته توخالی، و غیره) بر عدم تطابق فاز تأثیر می‌گذارد. علاوه‌براین، در طول فرایند تولید هارمونیک مرتبه بالا، الکترون‌ها شتاب می‌گیرند و برخی از آنها به یون اصلی خود بازمی‌گردند و در نتیجه انفجار پرتو ایکس ایجاد می‌شود. با این حال، اکثر این الکترون‌ها بر نمی‌گردند و در عوض به پراکندگی امواج مشترک کمک می‌کنند. الکترون‌های برگشتی به دلیل فرآیندهایی مانند یونیزاسیون، بازترکیبی و انتشار، فاز حمل می‌کنند. علاوه‌براین، اتم‌های یونیزه‌شده می‌توانند بر ضریب شکست محیط تأثیر بگذارند و منبع دیگری از پراکندگی را فراهم کنند.

عدم تطابق فاز را می‌توان به صورت زیر بیان کرد:

$Δ k = k_{q} - q k_{L} = \underset{< 0}{\underset{⏟}{Δ k_{n e u t r a l s}}} + \underset{< 0}{\underset{⏟}{Δ k_{i o n s}}} + \underset{> 0}{\underset{⏟}{Δ k_{e l e c t r o n s}}} + \underset{> 0}{\underset{⏟}{Δ k_{g e o m e t r y}}} + \underset{> 0}{\underset{⏟}{Δ k_{i n t r i n s i c}}} + \dots$

ه K_neutrals∆ سهم اتم‌های خنثی است، K_ions∆ سهم یون‌ها است (زمانی که خنثی‌ها یونیزه می‌شوند. این عبارت می‌تواند هنوز به اندازه کافی در اشعه UV باشد)، K_electrons∆ سهم پلاسما است، K_geometry∆ هندسه فوکوس آزاد است؛ صفحه هندسه هدایت موج، K_intrinsic∆ فازی است که توسط الکترون انباشته میشود در مدت زمانی که از اتم دور می‌شود. هر عبارت دارای یک علامت خاص است که اجازه می‌دهد تا عدم تطابق را در یک زمان و فرکانس خاص متعادل گردد [۴].

سهم الکترون‌ها به صورت درجه دوم با طول موج نیز به صورت زیر است: n_electrons = -λ²∆ در حالیکه سهم اتمها با طول موج معکوس میشود، n_atoms = λ^-2∆. بنابراین در طول موج‌های بلند IR، بخش n_electrons ∆ در هر الکترون بسیار بزرگ است، در حالیکه بخش n_atoms ∆ بسیار کوچک و نزدیک به یک است. برای تطبیق فاز فرایند HHG، فشارهای بسیار بالا و سطوح یونیزاسیون پایین مورد نیاز است؛ بنابراین تعداد زیادی ساطع‌کننده تولید می‌شود.

در محدوده طیفی UV قسمت n_atoms ∆ به دلیل اینکه رزونانس‌های UV نزدیک به هم است، بزرگ است، علاوهب‌ر این، عبارت n_electrons ∆ کوچک است. برای تطبیق فازی فرایند، فشارهای کم مورد نیاز است. همچنین، در اشعه UV، سطوح یونیزاسیون بسیار بالایی را می‌توان تحمل شود (بسیار بزرگتر از ۱۰۰٪). این عامل به انرژی فوتون HHG با شدت لیزر UV محرک، مقیاس‌پذیری می‌دهد. هندسه موج ساده یا هندسه با فوکوس ضعیف امکان تطبیق فاز خطی و استخراج حداکثر شار را در طول موج‌های محرک می‌دهد که عبارت کوچک است [۴].

تولید هارمونیک‌های مرتبه بالا در موجبر اجازه انتشار با ویژگی‌های نزدیک به انتشار موج صفحه را می‌دهد. چنین هندسه‌هایی مفید هستند؛ به‌ویژه طیف‌های اشعه ایکس تولیدشده توسط پرتوهای IR که در آن حجم‌های برهمکنش طولانی برای استخراج توان بهینه مورد نیاز است. در چنین هندسه‌هایی، طیف‌های eV 6/1تولید شده‌اند. برای هارمونیکهای مرتبه بالا مشتقشده از UV-VIS، عبارت موجبر کوچک است و تصویر تطبیق فاز شبیه هندسه موج صفحه است. در چنین هندسه‌هایی، هارمونیک‌ها پهنای باند باریکی که تا لبه کربن (eV 300) گسترش می‌یابند، تولید شده‌اند [۴].