مدل نورون بیولوژیک


مدل نورون بیولوژیک الگو:انگلیسیمعمولاً به عنوان یک مدل نورون اسپایک الگو:انگلیسی شناخته میشود، توضیحی ریاضی از خواص سلولهای خاص و مشخص در سیستم عصبی است که پتانسیلهای الکتریکی نیز در سراسر غشای سلولی خود ایجاد میکند در تقریباً یک میلی ثانیه ، همانطور که در شکل ۱ نشان داده مشاهده میکنید. نورون های اسپایک به عنوان یک واحد مهم سیگنالینگ سیستم عصبی شناخته میشوند و به همین دلیل توصیف عملکرد آنها از اهمیت بالایی برخوردار است. شایان ذکر است که تمام سلولهای سیستم عصبی نوع اسپایکی را تولید نمیکنند که در دامنه ی تعریفی مدل نورون های اسپایک تعریف شده است. به عنوان مثال سلولهای موی حلزون، سلولهای گیرنده شبکیه و سلولهای دو قطبی شبکیه اسپایک ندارند. علاوه بر این، بسیاری از سلولهای سیستم عصبی به عنوان سلولهای عصبی طبقهبندی نمیشوند بلکه درعوض به عنوان گلیا طبقهبندی می شوند. درنهایت، مدلهای عصبی بیولوژیکی با هدف بازگرداندن قابلیتهای کنترل از دست رفته مانند ادراک ، تصمیمگیری و کنترل مداوم اندام، مکانیسمهای اساسی عملکرد سیستم عصبی را توضیح میدهند. به این معنا، مدلهای نورون بیولوژیکی با مدلهای نورون مصنوعی که پیشبینی نتایج آزمایشهای مربوط به بافت عصبی بیولوژیکی فرض نمیشوند متفاوت است (اگرچه مدلهای نورون مصنوعی نیز به اجرای وظایف ادراک و تخمین مربوط هستند). بر این اساس، یک جنبه مهم از مدلهای نورون بیولوژیکی، اعتبار سنجی آزمایشی و استفاده از واحدهای فیزیکی برای توصیف روش آزمایشی مرتبط با پیشبینیهای مدل است.
مدلهای نورون را میتوان با توجه به واحدهای فیزیکی رابط مدل، به دو دسته تقسیم کرد. هر طبقه میتواند بیشتر با توجه به سطح انتزاع و جزئیات تقسیم شود:
- مدلهای ولتاژ غشایی ورودی-خروجی الکتریکی : این مدلها پیشبینی ولتاژ خروجی غشاها را به عنوان تابعی از تحریک الکتریکی در مرحله ورودی (یا ولتاژ یا جریان) تولید میکنند. مدلهای مختلف در این گروه در رابطه عملکردی دقیق بین جریان ورودی و ولتاژ خروجی و در سطح جزئیات متفاوت هستند. برخی از مدلهای این گروه مدلهای جعبه سیاه هستند و فقط بین دو سطح ولتاژ اندازهگیری شده تمایز قائل میشوند: وجود اسپایک یا حالت ساکن. مدلهای دیگر جزئیات بیشتری دارند و فرایندهای زیر سلولی را تشکیل میدهند.
- مدلهای نورون ورودی طبیعی یا دارویی : مدلهای این گروه بین محرک ورودی که میتواند دارویی یا طبیعی باشد، به احتمال وقوع اسپایک متصل میشوند. مرحله ورودی این مدلها الکتریکی نیست، بلکه دارای واحدهای تمرکز دارویی و شیمیایی یا واحدهای فیزیکی است که محرک خارجی مانند نور، صدا یا سایر اشکال فشار فیزیکی را توصیف میکند. علاوه بر این، مرحله خروجی نشان دهنده یک ولتاژ الکتریکی نیست بلکه نشان دهنده ی احتمال وقوع اسپایک است . معمولاً، این احتمال خروجی بهطور ثابت تقسیم بر یک زمان ثابت عادی میشود و احتمال عادی شده در نتیجه «سرعت شلیک یا آتش (به انگلیسی: Fire) » نامیده میشود و دارای واحد هرتز است. توصیف احتمالی گرفته شده توسط مدلهای این گروه از نتایج آزمایشی شامل تحریک طبیعی یا دارویی که دارای تغییرپذیری در الگوی اسپایک حاصل هستند، الهام گرفته شدهاست. با این وجود، وقتی میانگین این نتایج آزمایشی در چندین آزمایش انجام میشود، الگوی مشخصی اغلب آشکار میشود.
اگرچه در علم و مهندسی چند مدل توصیفی برای سطوح مختلف انتزاع وجود ندارد، اما تعداد مدلهای نورونهای مختلف، گاهی متناقض، بسیار زیاد است. این وضعیت تا حدودی نتیجه بسیاری از تنظیمات آزمایشی مختلف است . دشواری جدا کردن خصوصیات ذاتی یک نورون واحد از اثرات اندازهگیری و تعامل بسیاری از سلولها (اثرات شبکه) نیز مسبب این وضعیت نیز هست. برای تسریع همگرایی به یک نظریه واحد، ما در هر گروه چندین مدل را لیست میکنیم، و در صورت کاربرد، اشاراتی نیز به پشتیبانی از آزمایشها میکنیم.
مدلهای ولتاژ غشایی ورودی-خروجی برقی الگو:Anchor
مدلهای این گروه ارتباط بین جریانهای غشای عصبی در مرحله ورودی و ولتاژ غشای موجود در مرحله خروجی را توصیف میکنند. گستردهترین تحقیق تجربی در این دسته از مدلها توسط دو دانشمند به نام های هاچکین و هاکسلی در اوایل دهه ۱۹۵۰ با استفاده از یک آزمایش انجام شد که به خاطر نام این دو این دسته هاچکین-هاکسلی نامیده شد که پروسه تقریبی آزمایش این گونه بود با استفاده از یک آزمایش غشای سلولی را سوراخ شد و اجازه اعمال فشار یک ولتاژ یا جریان غشایی خاص را صادر شد.اکثر رابطهای عصبی برقی مدرن از تحریک الکتریکی خارج سلولی استفاده میکنند تا از سوراخ شدن غشاء که منجر به مرگ سلول و آسیب بافت میشود، تا حد امکان جلوگیری شود. از این رو، مشخص نیست که مدلهای نورون الکتریکی تا چه اندازه تحریک خارج سلولی را در خود نگه میدارند (به [۱] مراجعه کنید)
انباشت و شلیک (به انگلیسی: Integrate-and-fire)
یکی از اولین مدلهای توصیف رفتار یک نورون است که برای اولین بار در سال ۱۹۰۷ توسط لوئیس لاپیک بررسی شد. در این مدل، نورون به یک مدار شامل یک خازن و یک باتری تشبیه میشود که به صورت متوالی بسته شدهاند. باتوجه به قوانین الکترومغناطیس، توصیف این مدار به راحتی قابل انجام است. با گذشت زمان، خازن باردار شده و اگر مقدار بار صفحات خازن از حدی بیشتر شود، جرقهای بین دو صفحه خازن زده میشود و به این ترتیب بار خازن خالی می شود. مشابه این تخلیهی بار خازن، همان تیزه زدن نورون در دنیای واقعی است. همچنین باتری ذکر شده در مدار، مشابه کانالهای یونی غشای نورون است که اختلاف پتانسیل داخل و خارج غشا را به وسیلهی تغییر غلظت یونها تنظیم میکند. [۲]
که فقط مشتق قانون ظرفیت است ،الگو:Math. هنگامی که یک جریان ورودی اعمال میشود، ولتاژ غشایی با گذشت زمان افزایش مییابد تا اینکه به یک آستانه ثابت الگو:Math برسد، که در آن نقطه جرقهای بین صفحات خازن زده شده و خازن تخلیه میشود و ولتاژ را به پتانسیل استراحت خود بازنشانی میکند، پس از آن مدل همچنان به کار خود ادامه میدهد. فرکانس شلیک این مدل به طور خطی و بدون محدود شدن با افزایش جریان ورودی افزایش مییابد.
کاستی باقی مانده از این مدل این است که هیچ حافظه ای وابسته به زمان ندارد. اگر مدل مدتی سیگنال زیر آستانه را دریافت کند، آن را افزایش میدهد ولتاژ را برای همیشه حفظ میکند تا دوباره شلیک کند(معادلا نورون تیزه بزند.). این ویژگی به وضوح با رفتار عصبی مشاهده شده مطابقت ندارد.
| خاصیت مدل H&H | منابع |
|---|---|
| شکل اسپایک فردی است | [۳][۴][۵][۶] |
| هویت یونهای درگیر | [۳][۴][۵][۶] |
| سرعت اسپایک در سراسر آکسون | [۳] |
مدل هاجکین-هاکسلی (H&H مدل)[۳][۴][۵][۶]الگویی از رابطه جریان جریانهای یونی در غشای سلول عصبی و ولتاژ غشای سلول است.[۳][۴][۵][۶]این مجموعه شامل مجموعه ای از معادلات دیفرانسیل غیرخطی است که رفتار کانالهای یونی را که در غشای سلولی آکسون غول پیکر مرکب نفوذ میکنند، توصیف میکند. هاچکین و هاکسلی برای این کار جایزه نوبل فیزیولوژی یا پزشکی در سال ۱۹۶۳ دریافت کردند.
توجه داشته باشید که قبل از رابطه ولتاژ جریان ما، این بار تعمیم یافته است تا چندین جریان وابسته به ولتاژ را شامل شود:
هر جریان توسط قانون اهم به عنوان داده میشود
جایی کهالگو:Math رسانایی یا مقاومت معکوس است که میتواند از نظر میانگین ثابت الگو:Math گسترش یابد و به ترتیب کسری فعال سازی و غیرفعال سازی الگو:Math و الگو:Math تعیین میکند که چه تعداد یون میتواند از طریق کانالهای غشایی موجود جریان یابد. این بسط توسط فرمول
و بخشهایی از سینتیک مرتبه اول پیروی میکنند.
با دینامیک مشابه برای ساعت، که در آن ما میتوانیم از الگو:Math و الگو:Math یا الگو:Math و الگو:Math استفاده کنیم برای کسری دروازه خود را تعریف کنیم.
مدل هوچکین-هاکسلی ممکن است گسترش یابد تا جریانهای یونی اضافی را دربرگیرد. بهطور معمول، این شامل جریانهای ورودی Ca2+ and Na+ و Na+ به سمت داخل، و همچنین چندین نوع جریان K+ بیرونی از جمله جریان «نشت» است.نتیجه نهایی میتواند در ۲۰ پارامتر انتهای کوچک باشد که باید برای یک مدل دقیق تخمین زده یا اندازهگیری شود و برای سیستمهای پیچیده نورونهایی که به راحتی توسط کامپیوتر قابل ردیابی نیستند. در نتیجه سادهسازیهای دقیق مدل هوچکین-هاکسلی مورد نیاز است.
مدل انباشت و شلیک نشتی (به انگلیسی: Leaky integrate-and-fire)
مدل انباشت و شلیک نشتی، همچنین توسط لوئیز لاپیک[۷]مورد مطالعه قرار گرفتهاست، مشکل حافظه با اضافه کردن یک اصطلاح «نشت» به پتانسیل غشاء، حل میشود، و نشان دهندهی انتشار یونهایی است که در هنگام تیزه زدن از طریق غشای نورون با محیط خارج تبادل می شود.
در حقیقت ایرادی که به مدل قبلی وارد است ایده آل فرض کردن غشای سلولی است، در صورتی که وجود کانال های یونی به معنای تبادل یون ها و در نتیجه خازت ایده آل نبودن غشا است. این جریان ورودی حاصل از تبادل یون ها با محیط خارج باعث می شود که پتانسیل نورون از پتانسیل آستانه بیشتر شده و در نتیجه نورون تیزه می زند.
که برای جریانهای ورودی بزرگ به مدل بدون نشت قبلی همگرا میشود. این مدل همچنین میتواند به سلولهای عصبی مهاری گسترش یابد.
کسری ادغام شده و آتش (به انگلیسی: Fractional-order leaky integrate-and-fire)
پیشرفتهای اخیر در محاسبات کسری محاسباتی و نظری منجر به شکل جدیدی از مدل میشود، به نام کسری ادغام شده و آتش الگو:انگلیسی توسط تدانشمندی به نام تکا و همکارانش ایجاد شدهاست. مزیت بزرگ این مدل این است که میتواند تمام فعالیتهای گذشته را ضبط و یکپارچه کند و میتواند اقتباس های وابسته به زمان مشاهده شده در نورونهای هرمی را تولید کند. مدل دارای شکل زیر است . جزئیات بیشتری را میتوان در اینجا یافت.[۸]
Galves–Löcherbach
الگو:Main مدل Galves-Löcherbach یک توسعه خاص از مدل یکپارچه و آتش نشت است، ذاتاً تصادفی است. این مدل وسط آنتونیو گالوز و اوا لوچباخ ساخته شدهاست.[۹]با توجه به مشخصات مدل ، احتمال وجود دارد که نورون داده شده در یک بازه زمانی میلرزد ممکن است توسط
جایی که یکوزن سیناپسی است و تأثیر نورون را توصیف میکند روی نورون , نشت را بیان میکند و تاریخچه نورون اسپایک را قبل از فراهم میکند.البته با توجه به
ادغام و آتش نمایی(به انگلیسی: Exponential integrate-and-fire)
الگو:Main در مدل انتگرال و آتش نمایی، تولید اسپایک، به دنبال معادله نمایی است:
جایی که پتانسیل غشایی است ، آستانه بالقوه غشاء است ، زمان غشاء است. ثابت ، پتانسیل استراحت است. که درآن میزان وضوح ابتکار عمل پتانسیل ، معمولاً در حدود ۱ میلی ولت برای نورونهای هرمی قشر مغز است. هنگامی که پتانسیل غشاء از عبور کند، در زمان محدود به بینهایت منحرف میشود.[۱۰][۱۱][۱۲]
FitzHugh–Nagumo
الگو:Main سادهسازیها در مورد هاجکین-هاکسلی توسط FitzHugh و Nagumo در سال ۱۹۶۱ و ۱۹۶۲ معرفی شدند. به دنبال توصیف «خود تحریک احیا کننده» توسط یک ولتاژ غشای بازخورد مثبت و بازگرداندن توسط یک ولتاژ دروازه بازخورد منفی، آنها این مدل را توصیف کردند.
جایی که ما مجدداً دارای ولتاژ و جریان ورودی مانند غشاء با ولتاژ عمومی ورودی کندتر و پارامترهای تعیین شده آزمایشی a = -۰٫۷، b = ۰٫۸، τ = ۱ / ۰٫۰۸ هستیم. اگرچه به وضوح از زیستشناسی مشتق نشدهاست، مدل اجازه میدهد یک دینامیک ساده و فوراً در دسترس باشد، بدون اینکه بیاهمیت باشد.[۱۳]
Morris–Lecar
الگو:Main در سال ۱۹۸۱ موریس و لکار مدلهای هوچکین-هاکسلی و فیتز هیو-ناگومو را به یک مدل کانال کلسیم با ولتاژ دردار با یک کانال پتاسیم یکسوساز تأخیر، ترکیب کردند.
که در آن
Hindmarsh–Rose
الگو:Main با تکیه بر مدل FitzHugh-Nagumo , Hindmarsh و Rose در سال ۱۹۸۴ مدلی از فعالیت عصبی توصیف شده توسط سه معادله دیفرانسیل مرتبه اول همراه:
با الگو:Math, and الگو:Math به طوری که متغیر z فقط بسیار کند تغییر کند. این پیچیدگی ریاضی اضافی اجازه میدهد تا تنوع زیادی از رفتارهای پویا برای پتانسیل غشاء، شرح داده شده توسط متغیر x مدل، که شامل پویایی هرج و مرج است. این امر باعث میشود که مدل نورون Hindmarsh-Rose بسیار مفید باشد، زیرا هنوز ساده بودن، توصیف کیفی خوبی از الگوهای مختلف پتانسیل عمل مشاهده شده در آزمایشها را میدهد.
نظریه کابل
نظریه کابل، سنگ قبر دندریتیک را به عنوان یک ساختار استوانه ای که تحتالگوی منظم شکاف، که مانند شاخههای یک درخت قرار دارد، توصیف میکند. برای یک سیلندر منفرد یا یک درخت کامل، هدایت ورودی در پایه (جایی که درخت با بدن سلول یا هر مرز دیگری ملاقات میکند) تعریف میشود
جایی که الگو:Math طول الکتروتونیک استوانه است که به طول، قطر و مقاومت آن بستگی دارد. مقیاس بازگشتی ساده الگوریتم بهصورت خطی با تعداد شاخهها انجام میشود و میتواند برای محاسبه هدایت مؤثر درخت استفاده شود.
که در آن الگو:Math مساحت کل درخت از طول کل الگو:Math است، و الگو:Math طول کل الکتروتونیک آن است. برای یک نورون کل که در آن هدایت بدن سلول الگو:Math است و هدایت غشاء در هر واحد مساحت الگو:Math است، میتوانیم با با افزودن کلیه هدایت درخت و سوماً، میتوانیم هدایت نورونی کل الگو:Math را برای درختان دندریت الگو:Math پیدا کنیم.
جایی که میتوانیم با ذکر الگو:Math، فاکتور تصحیح کلی الگو:Math را به صورت تجربی پیدا کنیم.
مدلهای محاسباتی
الگو:See also مدل کابل برای ارائه نتایج تحلیلی بسته، تعدادی سادهسازی را ایجاد میکند، یعنی اینکه آبرور دندریتیک باید در یک الگوی ثابت در جفتهای کم رنگ شاخه ای داشته باشد. یک مدل محفظه ای امکان هر گونه توپولوژی درخت مورد نظر را با شاخهها و طولهای دلخواه فراهم میکند، اما در جابجایی بین شاخهها، سادهسازیها را انجام میدهد؛ بنابراین، دو مدل نتایج مکمل را ارائه میدهند، که هیچیک از آنها لزوماً دقیق تر نیستند.
هر قطعه جداگانه یا محفظه از یک دندریت توسط یک سیلندر مستقیم از طول الگو:Mathو قطر دلخواه الگو:Math مدل میشود که با مقاومت ثابت به هر تعداد سیلندر شاخه ای متصل میشود. نسبت هدایت سیلندر الگو:Mathth را به عنوان الگو:Math تعریف میکنیم، جایی که و الگو:Math مقاومت بین محفظه فعلی و بعدی است. ما یک سری معادلات را برای نسبتهای رسانایی در داخل و خارج از یک محفظه با انجام اصلاحات در دوره پویای عادی، الگو:Math بدست میآوریم.
جایی که آخرین معادله با والدین و دختران در شعب سر و کار دارد و . ما میتوانیم این معادلات را از طریق درخت تکرار کنیم تا جایی که نقطه ای که دندریتها به بدن سلولی متصل میشوند، که نسبت هدایت بن الگو:Math. بدست آوریم. سپس هدایت عصبی کل ما توسط داده میشود
(نمونه ای از مدل محفظه نورون، با الگوریتمی برای کاهش تعداد محفظهها (افزایش سرعت محاسبات) و در عین حال حفظ خصوصیات الکتریکی برجسته، میتوانید در [۱۴] ببینید.)
الگو:Anchor مدلهای نورون محرک ورودی طبیعی
مدلهای این گروه پس از آزمایشهای مربوط به تحریک طبیعی مانند نور، صدا، لمس یا بو بهوجود آمدهاند. در این آزمایشها، الگوی اسپایک ناشی از هر نمایش محرک از هر آزمایشی با آزمایشی دیگر متفاوت است، اما پاسخ متوسط از چندین آزمایش اغلب به یک الگوی واضح تبدیل میشود. در نتیجه، مدلهای این گروه یک رابطه احتمالی بین محرک ورودی به وقوع اسپایک ایجاد میکنند.
مدل فرایند پواسون غیر همگن (Siebert)
سیبریت[۱۵][۱۶] الگوی آتش (Fire) (به انگلیسی: Fire) اسپایک نورون با استفاده از یک مدل فرایند پواسون غیر همگن مدل، به دنبال آزمایشها مربوط به سیستم شنوایی است. به دنبال آزمایشها مربوط به سیستم شنوایی، الگوی آتش (Fire) (به انگلیسی: Fire) اسپایک نورون را با استفاده از یک مدل فرایند پواسون غیر همگن مدل کرد.[۱۵][۱۶]طبق گفته Siebert، احتمال وقوع اسپایک در فاصله زمانی متناسب با عملکرد غیر منفی است، جایی که محرک خام است:
سیبرت چندین عملکرد را به عنوان در نظر گرفت، از جمله برای شدت کم تحریک.
مهمترین مزیت مدل Siebert سادگی آن است. کاستی مدل عدم توانایی آن در بازتاب درست پدیدههای زیر است:
- لبه تأکید بر ویژگی نورون در پاسخ به نبض محرک.
- اشباع نرخ آتش..
- مقادیر فاصله اسپایک-فاصله-هیستوگرام در مقادیر فواصل کوتاه (نزدیک به صفر).
این کاستیها توسط مدل مارکوف دو ایالت بررسی شدهاست[۱۷][۱۸][۱۹]
مدل دو حالت مارکوف (Nossenson & Messer) الگو:Anchor
مدل نورون پرشکسته توسط Nossenson & Messer[۱۷][۱۸][۱۹] احتمال نورون را به آتش سوزی اسپایک به عنوان تابعی از محرک خارجی یا دارویی تولید میکند.[۱۷][۱۸][۱۹] این مدل شامل یک آبشار از یک مدل لایه گیرنده و یک مدل نورون اسپایک است، همانطور که در شکل ۴ نشان داده شدهاست. اتصال بین محرک خارجی با احتمال اسپایک در دو مرحله انجام میشود: اول، یک مدل سلول گیرنده محرک خارجی خام را ترجمه میکند. یک مدل نورون پرشور بین غلظت انتقال دهنده عصبی با میزان آتش (احتمال اسپایک) ارتباط مییابد؛ بنابراین، مدل نورون اسپایک به خودی خود به غلظت انتقال دهنده عصبی در مرحله ورودی بستگی دارد.[۱۷][۱۸][۱۹]

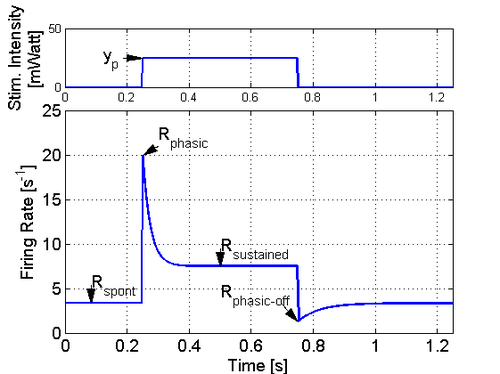
یکی از ویژگیهای مهم این مدل پیشبینی برای آتش (Fire) نورونهای الگوی سرعت آتش نورون است که با استفاده از تعداد کم پارامترهای آزاد، لبه مشخصه بر پاسخ نورونها به یک پالس محرک تأکید میکند، همانطور که در شکل ۵ نشان داده شدهاست. میزان آتش هر دو مشخص میشود. به عنوان یک احتمال عادی برای آتش اسپایک عصبی، و به عنوان یک مقدار متناسب با جریان انتقال دهندههای عصبی منتشر شده توسط سلول است. عبارت نرخ آتش به شکل زیر است:
جایی که،
- P0 احتمال وجود نورون «مسلح» و آماده آتش گرفتن است. این معادله دیفرانسیل زیر ارائه شدهاست:
P0 بهطور کلی میتواند بهصورت بازگشتی با استفاده از روش اویلر محاسبه شود، اما در صورت پالس محرک، یک عبارت ساده بسته بسته را نشان میدهد.[۱۷][۲۰]
- y(t) ورودی مدل است و به عنوان غلظت انتقال دهنده عصبی بر سلول اطراف آن (در بیشتر موارد گلوتامات) تعبیر میشود. برای یک محرک خارجی میتوان آن را از طریق مدل لایه گیرنده تخمین زد:
به دست آمده، با با میانگین زمانی کوتاه قدرت محرک (داده شده در وات یا انرژی دیگر در هر واحد زمان).
- R0 با میزان آتش (Fire) (به انگلیسی: Fire) خود به خودی نورون مطابقت دارد.
- R1 میزان بازیابی نورون از حالت نسوز است.
پیشبینیهای دیگر این مدل شامل موارد زیر است: ۱) بهطور متوسط پتانسیل پاسخ برانگیخته (ERP) به دلیل جمعیت تعداد زیادی از نورونها در اندازهگیریهای فیلتر نشده شبیه سرعت آتش (Fire) (به انگلیسی: Fire) است[۱۹]
۲) واریانس ولتاژ فعالیت ناشی از فعالیت نورونهای متعدد شبیه به میزان آتش است (همچنین به عنوان قدرت چند منظوره یا MUA شناخته میشود).[۱۸][۱۹]
۳) توزیع احتمال فاصله میان اسپایک شکل یک توابع توزیع گاما مانند عملکرد را به خود میگیرد.[۱۷][۲۰]
| خاصیت مدل توسط Nossenson & Messer | منابع | توضیحات شواهد تجربی |
|---|---|---|
| شکل میزان آتش گرفتن در پاسخ به یک نبض محرک شنوایی | [۲۱][۲۲][۲۳][۲۴][۲۵] | نرخ آتش همان شکل ۵ را دارد. |
| شکل میزان آتش شدن در پاسخ به یک نبض محرک بصری | [۲۶][۲۷][۲۸][۲۹] | نرخ آتش همان شکل ۵ را دارد. |
| شکل میزان آتش شدن در پاسخ به یک نبض محرک بویایی | [۳۰] | نرخ آتش همان شکل ۵ را دارد. |
| شکل میزان آتش در پاسخ به یک محرک احساس حسی | [۳۱] | نرخ آتش همان شکل ۵ را دارد. |
| تغییر میزان آتش در پاسخ به برنامه انتقال دهنده عصبی (عمدتاً گلوتامات) | [۳۲][۳۳] | تغییر نرخ آتش در پاسخ به برنامه انتقال دهنده عصبی (گلوتامات) |
| وابستگی مربعی بین فشار محرک شنوایی و میزان آتش | [۳۴] | وابستگی مربع بین فشار محرک شنوایی و میزان آتش ( وابستگی خطی در مربع فشار (قدرت)). |
| وابستگی مربعی بین میدان الکتریکی محرک بصری (ولت) و میزان آتش | [۲۷] | وابستگی مربع بین میدان الکتریکی محرک بصری (ولت) - وابستگی خطی بین قدرت تحریک بصری و میزان آتش. |
| شکل آمار Inter-Spike-Interval (ISI) | [۳۵] | شکل ISI شبیه عملکرد گاما است |
| ERP در اندازهگیریهای فیلتر نشده شبیه میزان آتش است | [۳۶] | شکل پتانسیل پاسخ برانگیخته بهطور متوسط در پاسخ به محرک شبیه به میزان آتش است (شکل ۵). |
| قدرت MUA به میزان آتش شباهت دارد | [۱۹][۳۷] | شکل واریانس تجربی اندازهگیریهای خارج سلولی در پاسخ به پالس محرک شبیه میزان آتش است (شکل ۵). |
الگو:Anchor مدلهای نورون محرک ورودی دارویی
مدلهای این گروه پیشبینیهایی را برای آزمایشهای مربوط به تحریک دارویی ارائه میدهند.
انتقال سیناپسی (Koch & Segev)
الگو:See also طبق مدلی که توسط کوچ و سگف انجام شد، پاسخ یک نورون به انتقال دهندههای عصبی فردی را میتوان به عنوان یک الگوی پسوند مدل کلاسیک هاچکین-هاکسلی با هر دو جریان جنبشی استاندارد و غیر استاندارد مدل کرد. چهار انتقال دهنده عصبی در درجه اول در CNS تأثیر دارند. گیرندههای AMPA / kainate واسطه تحریکی سریع هستند در حالی که گیرندههای NMDA واسطه جریانهای بهطور قابل توجهی کندتر هستند. جریان مهاری سریع از طریق گیرندههای GABAA receptors عبور میکند، در حالی که گیرندههای GABAB receptors توسط کانالهای پتاسیم فعال شده با پروتئین G واسطه میشوند. این طیف میانجیگری دینامیک فعلی را تولید میکند:
جایی که الگو:Math [۳]رسانایی (در حدود 1S) و E پتانسیل تعادل یون یا فرستنده داده شده (AMDA , NMDA , Cl یا K) بیشینه است، در حالی که الگو:Math کسری از گیرندههای باز را توصیف میکند. برای NMDA، یک اثر قابل توجهی از بلوک منیزیم وجود دارد که بهطور متفاوتی به غلظت منیزیم داخل سلولی توسط الگو:Math بستگی دارد. از نظر GABAB, الگو:Math غلظت پروتئین G است والگو:Math تفکیک G در اتصال به دروازههای پتاسیم را توصیف میکند.
پویایی این مدل پیچیدهتر به صورت تجربی مورد مطالعه قرار گرفتهاست و از نظر تقویت سیناپسی بسیار سریع است و افسردگی،به معنای یادگیری سریع، کوتاه مدت است.
مدل دو حالت مارکوف (Nossenson & Messer)
مدل توسط Nossenson و Messer غلظت انتقال دهنده عصبی را در مرحله ورود به احتمال آزاد شدن انتقال دهنده عصبی در مرحله خروجی ترجمه میکند.[۱۷][۱۸][۱۹]
برای توضیحات بیشتر در مورد این مدل، به بخش دو حالت مارکوف مدل بالا مراجعه کنید..
مدل نورون HTM
مدل نورون HTM توسط جف هاوکینز و محققان Numenta ساخته شدهاست و مبتنی بر نظریه ای به نام حافظه موقت سلسله مراتبی است که در ابتدا در کتاب On Intelligence شرح داده شدهاست. این مبتنی بر علوم اعصاب و فیزیولوژی و تعامل نورونهای هرمی در نئوکورتکس مغز انسان است.
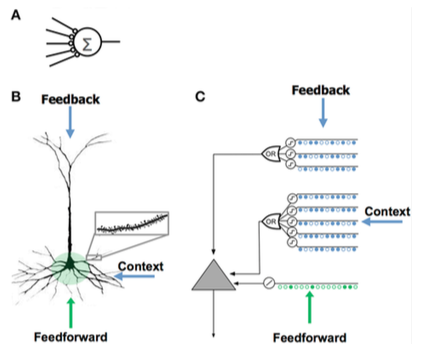
| الگو:وسطچینشبکه عصبی مصنوعی (ANN)الگو:پایان | الگو:وسطچیننورون هرمی نئوکورتیکال (نورون بیولوژیکی)الگو:پایان | الگو:وسطچیننورون مدل HTMالگو:پایان |
| - چند سیناپس
- بدون دندریت - جمع وزنهای ورودی x - با اصلاح وزن سیناپسها میآموزد |
-
- دندریتهای فعال: سلول صدها الگوی منحصر به فرد را تشخیص میدهد - فعال شدن مجموعه ای از سیناپسها بر روی یک قطعه دندریتیک باعث ایجاد سنبله NMDA و دپلاریزاسیون در سوماً میشود. - منابع ورودی به سلول:
- با رشد سیناپسهای جدید میآموزد |
- با الهام از سلولهای هرمی در لایههای neocortex 2/3 و ۵
- هزاران سیناپس - دندریتهای فعال: سلول صدها الگوی منحصر به فرد را تشخیص میدهد - دندریتهای مدل و سنبلههای NMDA با هر مجموعه از آشکارسازهای تصادفی که دارای یک مجموعه سیناپس هستند - آموختن با مدل سازی رشد سیناپسهای جدید |
رابطه بین مدلهای عصبی مصنوعی و بیولوژیکی
اساسیترین مدل یک نورون شامل یک ورودی با مقداری بردار وزن سیناپسی و یک تابع فعال سازی یا عملکرد انتقال در داخل خروجی تعیینکننده نورون است. این ساختار اساسی است که برای نورونهای مصنوعی به کار میرود، که در یک شبکه عصبی اغلب به نظر میرسد
در جایی که الگو:Math خروجی نورون الگو:Mathth است ،الگو:Math سیگنال نورون ورودی الگو:Mathth است، الگو:Math وزن سیناپسی (یا قدرت اتصال) بین نورونهای i و j است، و φ عملکرد فعال سازی است. در حالی که این مدل در برنامههای کاربردی یادگیری ماشین موفقیتی داشتهاست، این یک الگوی ضعیف برای نورونهای واقعی (بیولوژیکی) است، زیرا فاقد وابستگی زمانی است که اسپایکهای نورون واقعی به نمایش میگذارد. مدلهای بیولوژیکی از نوع «یکپارچه و آتش » اساساً این شکل را به خود میگیرند. در ادبیات پزشکی و دارویی آنها تا حد زیادی توسط مدلهای جنبشی مانند مدل هوچکین-هاکسلی جانشین شدهاند.در مورد مدل سازی یک نورون بیولوژیکی، از آنالوگهای فیزیکی به جای انتزاعهایی مانند «وزن» و «عملکرد انتقال» استفاده میشود. یک نورون پر از آب است و حاوی یونهایی است که بار الکتریکی دارند. نورون توسط یک غشای سلولی عایق محدود شده و میتواند غلظت یونهای بارشی را از هر طرف که تعیینکننده یک الگو:Math ظرفیت خازن است، حفظ کند. آتش یک نورون شامل حرکت یونها به داخل سلول است که وقتی انتقال دهندههای عصبی باعث میشوند کانالهای یونی در غشای سلولی باز شوند رخ میدهد. ما این موضوع را با یک جریان فیزیکی وابسته به زمان الگو:Math توصیف میکنیم. با این کار تغییر ولتاژ یا اختلاف انرژی پتانسیل الکتریکی بین سلول و محیط اطراف آن مشاهده میشود که گاهی اوقات منجر به ایجاد سنسور ولتاژ به نام پتانسیل عمل میشود که طول سلول را طی میکند و باعث ترشح انتقال دهندههای عصبی بیشتر میشود. ولتاژ، بنابراین مقدار علاقه است و توسطالگو:Math داده میشود.
حدس دربارهٔ نقش نورون در زمینه وسیع تر از اصل عمل مغز
طرح تشخیص انرژی مبتنی بر انتقال دهنده عصبی
طرح تشخیص انرژی مبتنی بر انتقال دهنده عصبی[۲۰] نشان میدهد که بافت عصبی شیمیایی یک روش تشخیص رادار مانند را انجام میدهد.

همانطور که در شکل ۶ نشان داده شدهاست، ایده اصلی حدس حساب این است که غلظت انتقال دهندههای عصبی، تولید انتقال دهندههای عصبی و انتقال مواد انتقال دهنده عصبی را به عنوان مقادیر مهم در انجام کار تشخیص، حساب کند، در حالی که اشاره به پتانسیلهای الکتریکی اندازهگیری شده به عنوان یک اثر جانبی که فقط در موارد مشخص است شرایط همزمان با هدف کاربردی هر مرحله است. طرح تشخیص شبیه به یک رادار مانند «تشخیص انرژی» است زیرا شامل مربع سیگنال، جمع شدن موقتی و مکانیزم سوئیچ آستانه است،درست مثل آشکارساز انرژی، اما شامل واحدی نیز میشود که بر لبههای محرک و طول حافظه متغیر (حافظه متغیر) تأکید میکند. مطابق این حدس، معادل فیزیولوژیکی آمار آزمایش انرژی، غلظت انتقال دهنده عصبی است و میزان آتش با جریان انتقال دهنده عصبی مطابقت دارد. مزیت این تفسیر این است که منجر به یک توضیح مداوم در واحد میشود که میتواند بین اندازهگیریهای الکتروفیزیولوژیکی، اندازهگیریهای بیوشیمیایی و نتایج روان شناختی ارتباط برقرار کند.
شواهد بررسی شده در [۱۹][۲۰] ارتباط زیر را بین عملکرد و طبقهبندی بافتشناسی نشان میدهد:
- مربع محرک احتمالاً توسط سلولهای گیرنده انجام میشود.
- لبه تحریک و انتقال سیگنال توسط سلولهای عصبی انجام میشود.
- تجمع موقت انتقال دهندههای عصبی توسط سلولهای گلیا انجام میشود. تجمع کوتاه مدت انتقال دهنده عصبی احتمالاً در برخی از انواع نورونها نیز رخ میدهد.
- سوئیچینگ منطقی توسط سلولهای گلیا انجام میشود و نتیجه آن بیش از حد آستانه غلظت انتقال دهنده عصبی است. این گذر آستانه همچنین با تغییر در سرعت نشت انتقال دهندههای عصبی همراه است.
- جابجایی کلی یا غیر حرکتی بدنی به دلیل سلولهای عضلانی است و نتیجه آن از تجمع بیش از حد آستانه غلظت انتقال دهنده عصبی بر محیط عضلانی است.
توجه داشته باشید که اگرچه سیگنالهای الکتروفیزیولوژیکی در شکل ۶ اغلب شبیه سیگنال عملکردی (قدرت سیگنال / غلظت انتقال دهنده عصبی / نیروی عضلانی) هستند، اما برخی مراحل وجود دارد که مشاهده الکتریکی با هدف عملکردی مرحله مربوطه متفاوت است. به طور خاص Nossenson و همکاران او، پیشنهاد کردند که عبور آستانه گلیا در مقایسه با سیگنال الکتروفیزیولوژیکی تابش شده دارای عملکردی کاملاً متفاوت است و ممکن است دومی تنها یک عارضه جانبی شکست گلیا باشد.
نظرات کلی در مورد دیدگاه مدرن مدلهای علمی و مهندسی
- مدلهای بالا هنوز ایدهآل هستند.دمای مورد نظر باید اصلاح شود برای افزایش سطح غشای سطح غده های دندریتیک ، درجه حرارت قابل توجهی گرم تر از داده های آزمایشی دمای اتاق و غیر یکنواختی در ساختار داخلی سلول است. برخی از جلوههای مشاهده شده در بعضی از این مدلها جای ندارند. به عنوان مثال، چرخه ی دما (با حداقل افزایش دمای خالص) غشای سلولی در طول تکثیر پتانسیل، با مدلهایی که به مدل سازی غشاء به عنوان یک مقاومت متکی هستند که باید در جریان از انرژی متکی باشد، سازگار نیست. ضخیم شدن موقت غشای سلولی در طول تکثیر پتانسیل عمل نیز توسط این مدلها پیشبینی نشدهاست، و همچنین ظرفیت و ولتاژ در حال تغییر که نتیجه این ضخیم شدن است، در این مدلها گنجانیده نشدهاست. عمل برخی از داروهای بیحسی مانند گازهای بی اثر برای این مدلها نیز مشکل ساز است. مدلهای جدید مانند مدل soliton سعی در توضیح این پدیدهها دارند، اما نسبت به مدلهای قدیمی توسعه کمتری دارند و هنوز کاربرد گستردهای ندارند.
دیدگاههای مدرن در مورد نقش مدل علمی نشان میدهد که «همه مدلها اشتباه هستند اما برخی مفید هستند» حدس اخیر نشان میدهد که هر نورون ممکن است به عنوان مجموعه ای از واحدهای آستانه مستقل عمل کند. پیشنهاد میشود که یک نورون به دنبال منشأ سیگنالهای وارد شده به غشاء، از طریق درختان دندریتیک خود، ناهمسانگردی فعال شود. همچنین فرم موج اسپایک وابسته به منشأ محرک پیشنهاد شدهاست. [۳۸]
منابع
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ ۳٫۰ ۳٫۱ ۳٫۲ ۳٫۳ ۳٫۴ ۳٫۵ الگو:Cite journal
- ↑ ۴٫۰ ۴٫۱ ۴٫۲ ۴٫۳ الگو:Cite journal
- ↑ ۵٫۰ ۵٫۱ ۵٫۲ ۵٫۳ الگو:Cite journal
- ↑ ۶٫۰ ۶٫۱ ۶٫۲ ۶٫۳ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ ۱۵٫۰ ۱۵٫۱ الگو:Cite journal
- ↑ ۱۶٫۰ ۱۶٫۱ الگو:Cite journal
- ↑ ۱۷٫۰۰ ۱۷٫۰۱ ۱۷٫۰۲ ۱۷٫۰۳ ۱۷٫۰۴ ۱۷٫۰۵ ۱۷٫۰۶ ۱۷٫۰۷ ۱۷٫۰۸ ۱۷٫۰۹ الگو:Cite book
- ↑ ۱۸٫۰ ۱۸٫۱ ۱۸٫۲ ۱۸٫۳ ۱۸٫۴ ۱۸٫۵ ۱۸٫۶ الگو:Cite journal
- ↑ ۱۹٫۰۰ ۱۹٫۰۱ ۱۹٫۰۲ ۱۹٫۰۳ ۱۹٫۰۴ ۱۹٫۰۵ ۱۹٫۰۶ ۱۹٫۰۷ ۱۹٫۰۸ ۱۹٫۰۹ ۱۹٫۱۰ ۱۹٫۱۱ ۱۹٫۱۲ الگو:Cite journal
- ↑ ۲۰٫۰ ۲۰٫۱ ۲۰٫۲ ۲۰٫۳ ۲۰٫۴ الگو:Cite book
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ ۲۷٫۰ ۲۷٫۱ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal
- ↑ الگو:Cite journal