مرتب‌سازی ادغام-درج

الگو:ادغام از در علوم رایانه، مرتب‌سازی ادغام-درج یا الگوریتم فورد-جانسون از الگوریتم‌های مرتب‌سازی مقایسه‌ای است که در سال ۱۹۵۹ توسط لستر رادولف فورد و سلمر مارتین جانسون منتشر شد. این الگوریتم از الگوریتم‌های شناخته شده قبلی همچون مرتب‌سازی درجی دودویی و مرتب‌سازی ادغامی در بدترین حالت، از تعداد مقایسه‌های کمتری استفاده می‌کند.

مشخص است که کم بودن تعداد مقایسه‌ها معیاری مناسب برای اثربخشی یک الگوریتم مرتب‌سازی نیست؛ امّا از دیدگاه نظری کمینه کردن تعداد مقایسه‌ها در مسائل مرتب‌سازی همواره مهم بوده‌است. همین الگوریتم توسط ریاضیدان لهستانی به‌طور مستقل کشف شد.

مقدمه ای بر الگوریتم

فرض می‌کنیم ۵ عدد داریم ($a,b,c,d,e$)، آن‌ها را به سه دسته تقسیم می‌کنیم: $(a,b)(c,d)(e)$

سپس دو عدد موجود در دسته‌های دوتایی را باهم مقایسه می‌کنیم و بعد از آن دو عدد بزرگتر هر دسته را با یکدیگر مقایسه می‌کنیم. فرض می‌کنیم

$a>b,c>d$

. آنگاه باید دو عدد

$a,c$

را با هم مقایسه کنیم. در شکل‌های زیر جهت پیکان از عدد کوچکتر به سمت عدد بزرگتر است.الگو:سخ

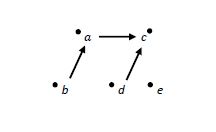
با توجه به شکل بالا داریم $b<a<c$. اکنون باید عنصر $e$ را بین این سه عنصر مرتب شده درج کنیم که با دو مقایسه امکان‌پذیر است. (مرتب‌سازی درجی دودویی) سپس بعد از معلوم شدن جایگاه $e$، عنصر $d$ را در صف مرتب شده درج می‌کنیم که آن نیز با دو مقایسه امکان‌پذیر است.

الگوریتم

الگوریتم فورد-جانسون یا مرتب‌سازی ادغام-درج تعمیم جالبی از مقدمه بالاست. مراحل این الگوریتم به شرح زیر است:

ادغام

1. $n$ عنصر موجود را به $\lfloor \frac{n}{2}\rfloor$ گروه دوتایی تقسیم می‌کنیم؛ و اگر $n$ فرد بود، یک عنصر جفت نشده باقی می‌ماند.
2. $\lfloor \frac{n}{2}\rfloor$مقایسه انجام می‌دهیم تا عنصر بزرگتر در هر گروه را بیابیم.
3. $\lfloor \frac{n}{2}\rfloor$ عنصر بزرگتر را به شکل بازگشتی مرتب می‌کنیم. حال عناصر مرتب شده را زنجیره اصلی می‌نامیم که به صورت $a_i$در شکل نمایش داده شده‌است.

   

4. سپس با توجه به این که زنجیره اصلی مرتب شده‌است و عنصر $a_1$ کوچکترین عنصر زنجیره است و می‌دانیم $b_1$ از آن کوچکتر است، بنابراین می‌توان $b_1$ را در ابتدای زنجیره درج نمود.
5. بقیه عناصر که به شکل $b_i$ نشان داده شده‌است را در زنجیره اصلی درج می‌کنیم. (با استفاده از مرتب‌سازی درجی)

درج

روش درج کردن $b_i$ها به ترتیب زیر است:الگو:وسط‌چین $b_3,b_2;b_5,b_4;b_{1}1,b_{1}0,...,b_6;.....;b_{t_k},b_{t_{k-1}},......,b_{t_{k-1}}+1$

$(t_1,t_2,t_3,t_4,...)=(1,3,5,11,...)$ الگو:پایانسپس در آخر در صورت وجود، $b_{\lfloor \frac{n}{2}\rfloor +1}$ را در زنجیره اصلی درج می‌نماییم.

تحلیل الگوریتم

برای بررسی تعداد مقایسه‌ها ابتدا به مقادیر $t_k$ها می‌پردازیم. این مقادیر باید باید به گونه‌ای باشند که تعداد عناصر زنجیره اصلی هنگام درج یک عنصر در مرحله $k$ام برابر $2^k-1$باشد.

در نتیجه داریم:الگو:وسط‌چین $2t_{k-1}+(t_k-t_{k-1})-1=2^k-1⟹t_k+t_{k-1}=2^k,t_1=1$ الگو:پایانبا حل رابطه بازگشتی بالا به جواب زیر می‌رسیم:الگو:وسط‌چین $t_k=\frac{1}{3}(2^{k+1}+(-1{)}^k)$ الگو:پایان$F(n)$را تعداد مقایسه‌های الگوریتم فورد-جانسون برای $n$عنصر می‌گیریم. ابتدا $\lfloor \frac{n}{2}\rfloor$مقایسه برای پیدا کردن عنصر بزرگتر در هر دسته داریم و سپس زنجیره اصلی را به شکل بازگشتی مرتب می‌کنیم و $G$هم تعداد مقایسه‌ها برای درج عناصر کوچکتر دسته‌ها در زنجیره اصلی است.الگو:وسط‌چین $F(n)=\lfloor \frac{n}{2}\rfloor +F(\lfloor \frac{n}{2}\rfloor )+G(\lceil \frac{n}{2}\rceil )$ الگو:پایانو برای هر $t_{k-1}\le n\le t_k$،$G(n)$برابر است با $\sum _{j=1}^{k-1}[j(t_j-t_{j-1})]+k(n-t_{k-1})$.الگو:وسط‌چین $\sum _{j=1}^{k-1}[j(t_j-t_{j-1})]+k(n-t_{k-1})=kn-(t_0+t_1+t_2+...+t_{k-1})$

$w_k=t_0+t_1+t_2+...+t_{k-1}⟹(w_0,w_1,w_2,w_3,...)=(0,1,2,5,...)$ الگو:پایانپس از تعریف $w_k$به شکل بالا می‌توان ثابت کرد : $F(n)-F(n-1)=k⟺w_k<n\le w_{k+1}$

و شرط بالا معادل است با : $\frac{2^{k+1}}{3}<n<\frac{2^{k+2}}{3}⟹k+1<log(3n)\le k+2$

بنابرابن داریم : $F(n)-F(n-1)=\lceil log(\frac{3}{4}n)\rceil$

در نتیجه: $F(n)=\sum _{k=1}^n\lceil log(\frac{3}{4}k)\rceil$

مقایسه با سایر الگوریتم‌ها

نام این الگوریتم ادغام-درج است زیرا مقایسه‌های اولیه که قبل از فراخوانی بازگشتی انجام می‌شود، همچون مقایسه‌های الگوریتم مرتب‌سازی ادغامی است و همچنین مقایسه‌هایی که بعد از فراخوانی بازگشتی صورت می‌گیرد، مانند الگوریتم مرتب‌سازی درجی دودویی است. در واقع می‌توان الگوریتم فورد-جانسون را الگوریتم چندگانه نامید زیرا تلفیقی از دو مرتب‌سازی درجی و ادغامی است.

تعداد مقایسه‌های این الگوریتم مرتب‌سازی برای $n\le 11$برابر با کران پایین تعداد مقایسه‌های مرتب‌سازی‌های مقایسه‌ای است. این کران پایین برابر است با $\lceil {\log }_{2}n!\rceil \approx n{\log }_{2}n-1.443n$

امّا تعداد مقایسه برای $n$های بزرگتر بیشتر از این کران پایین است.

همان‌طور که در جدول زیر دیده می‌شود، تعداد مقایسه‌ها در الگوریتم فورد-جانسون از دو الگوریتم ادغامی و درجی برای $n$های کوچکتر از $18$ کمتر است.الگو:سخ

تعداد مقایسه‌ها در بدترین حالت

۱۷	۱۶	۱۵	۱۴	۱۳	۱۲	۱۱	۱۰	۹	۸	۷	۶	۵	۴	۳	۲	۱	n
۵۴	۴۹	۴۵	۴۱	۳۷	۳۳	۲۹	۲۵	۲۱	۱۷	۱۴	۱۱	۸	۵	۳	۱	۰	مرتب‌سازی درجی
۶۵	۴۹	۴۵	۴۱	۳۸	۳۳	۳۰	۲۷	۲۵	۱۷	۱۴	۱۱	۹	۵	۳	۱	۰	مرتب‌سازی ادغامی
۵۰	۴۶	۴۲	۳۸	۳۴	۳۰	۲۶	۲۲	۱۹	۱۶	۱۳	۱۰	۷	۵	۳	۱	۰	مرتب‌سازی ادغام-درج

الگوریتم‌های بهینه تر

تا به امروز الگوریتم بهینه‌تر از نظر زمانی برای الگوریتم فورد-جانسون ارائه شده‌است که تعداد مقایسه‌های دقیقاً برابر فورد-جانسون است؛ امَا زمان کمتری می‌گیرد بدین گونه که به جای فراخوانی بازگشتی بر روی نصف لیست اعداد، بر روی یک چهارم لیست اعداد می‌باشد.

تا بیست سال الگوریتم فورد-جانسون، کمترین تعداد مقایسه را میان الگوریتم‌های مرتب‌سازی داشت. در سال ۱۹۷۹ گلن ماناکر الگوریتم مرتب‌سازی دیگری ارائه کرد که تعداد مقایسه‌های آن از فورد-جانسون حتی برای ورودی‌ها با تعداد زیاد نیز کمتر بود.

ماناکر نشان داد الگوریتم فورد-جانسون برای محدوده‌ای از مقادیر بهینه است. امروزه الگوریتمی ارائه شده‌است که به نتایج قوی‌تری نسبت به الگوریتم ماناکر دست یافته‌است.