بردار پوئینتینگ

بردار پوئینتینگ

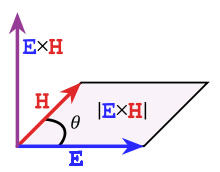
بردار پوینتینگ، نامِ برداری در فیزیک است. اندازهٔ این بردار، چگالیِ انرژیِ الکترومغناطیسی‌ را نشان می‌دهد که از واحدِ سطح در واحدِ زمان عبور می‌کند و واحدِ آن وات بر مترِ مربع (W/m²) است. این بردار، به نامِ کسی که آن را به دست آورد، فیزیک‌دان انگلیسی جان پوینتینگ، نام‌گذاری شده‌است. این بردار از طریقِ رابطهٔ زیر، با میدانِ الکتریکی و میدانِ مغناطیسی، پیوند می‌یابد: الگو:چپ‌چین

$𝐒=\frac{1}{{\mu }_0}𝐄\times 𝐁$

الگو:پایان چپ‌چین که در آن:

• $𝐒$ نشان‌دهندهٔ بردارِ پوینتینگ است.
• $𝐄$ نشان‌دهندهٔ بردارِ میدانِ الکتریکی است.
• $𝐁$ نشان‌دهندهٔ بردارِ میدانِ مغناطیسی است.

رابطه‌ها و اثبات آن‌ها

جان هنری پوینتینگ فیزیکدان انگلیسی.بردار پوینتینگ حاصل تلاش های وی بوده که به نام او،نامگذاری شده.

اندازه بردار پوینتینگ

چگالیِ انرژیِ الکتریکی و چگالیِ انرژیِ مغناطیسی‌ که در یک سیستم ذخیره شده‌است، هر کدام به ترتیب از رابطه‌هایِ زیر به دست می‌آیند: الگو:چپ‌چین

$u_e=\frac{1}{2}{\epsilon }_0{\left|𝐄\right|}^2$

$u_m=\frac{1}{2}\frac{{\left|𝐁\right|}^2}{{\mu }_0}$

الگو:پایان چپ‌چین در نتیجه چگالیِ انرژیِ کلِ ذخیره شده در فضا، عبارت است از: الگو:چپ‌چین

$u=\frac{1}{2}({ϵ}_0{\left|𝐄\right|}^2+\frac{{\left|𝐁\right|}^2}{{\mu }_0})$

الگو:پایان چپ‌چین موجِ الکترومغناطیسی در خلاء با سرعتِ نور منتشر می‌شود که آن را با c نمایش می‌دهیم. در بازه‌یِ زمانیِ $\mathrm{\Delta }t$، این موج به اندازهٔ $c\mathrm{\Delta }t$ به جلو رفته‌است. اگر یک میدانِ پیوستهٔ الکترومغناطیسی را در نظر بگیریم که در یک بازهٔ زمانیِ معین به سطحی با مساحتِ A می‌تابد، آن‌گاه از هر واحدِ سطح، طولِ $c\mathrm{\Delta }t$ از میدانِ الکترومغناطیسی عبور کرده‌است. اگر انرژی هر واحد از طولِ عبور کرده برابر با u که همان چگالیِ انرژی است باشد آن‌گاه انرژیِ کلِ عبور کرده در واحدِ سطح در یک بازهٔ زمانیِ برابر خواهد بود: $u\left(\text{c}\mathrm{\Delta }t\right)$ با تقسیم کردنِ انرژیِ کلِ عبوری بر زمانی که این انرژی عبور کرده‌است، انرژیِ کلِ عبور کرده از واحدِ سطح، در واحدِ زمان، به دست می‌آید: الگو:چپ‌چین

$\left|𝐒\right|=uc$

$\left|𝐒\right|=\frac{1}{2}\text{c}({ϵ}_0{\left|𝐄\right|}^2+\frac{{\left|𝐁\right|}^2}{{\mu }_0})$

الگو:پایان چپ‌چین حال با توجه به اینکه $c^2=\frac{1}{{\mu }_0{\epsilon }_0}$ به راحتی می‌توان نشان داد که : $u_m$ و $u_e$ با هم برابر هستند. به علاوه، از آن‌جایی که موجِ الکترومغناطیسی، موجی عرضی است، میدان‌هایِ الکتریکی و مغناطیسیِ آن برهم عمود هستند و می‌توان نشان داد که $\left|𝐄\right|=c\left|𝐁\right|$ در نتیجه با جایگذاریِ این دو رابطه در رابطهٔ بالا، رابطهٔ نهایی برایِ اندازه‌یِ بردارِ پوینتینگ این‌گونه به دست می‌آید: الگو:چپ‌چین

$\left|𝐒\right|=\frac{1}{{\mu }_o}\left|𝐄\right|\left|𝐁\right|$

دیگر رابطه‌ها

بردارِ پوینتینگ، که از تعمیمِ این رابطه به بردارها ساخته شده‌است، برداری است که جهتِ آن، جهتِ سطحِ عبوری را نشان می‌دهد -با توجه به عمود بودنِ میدانِ الکتریکی و مغناطیسی برهم و عرضی بودنِ موج. - و اندازهٔ آن، اندازهٔ انرژیِ عبوری از واحدِ سطح را در واحدِ زمان نشان می‌دهد. با توجه به آن‌که $𝐁={\mu }_0𝐇$، این بردار، آن‌طور که خودِ جان پوینتینگ، آن را نمایش می‌داد و به فرمِ آبراهام معروف است، خواهد بود: الگو:چپ‌چین

$𝐒=𝐄\times 𝐇,$

الگو:پایان چپ‌چین یکی از دلایلِ اهمیتِ این بردار، این است که به کمکِ آن، می‌توان بسیاری از کمیت‌هایِ دیگر را به راحتی، محاسبه کرد. یکی از مهم‌ترینِ این کمیت‌ها، تابندگی یا چگالیِ تابشداری الگو:به انگلیسی است که از میانگینِ گرفتنِ اندازهٔ S در یک دورهٔ تناوب به دست می‌آید: الگو:چپ‌چین

$I={⟨S⟩}_T=\frac{1}{2}{\epsilon }_0{\left|𝐄\right|}^2$

منابع

1. هشت، یوگن؛ Optics، ویرایش چهارم، صفحهٔ ۵۴ تا ۵۷
2. ریتس، جان؛ فردریک میلفورد و رابرت کریستی؛ مبانی نظریه الکترومغناطیس؛ ویرایش سوم، ترجمهٔ جلال صمیمی، نشر مرکز، صفحهٔ ۴۳۱
3. الگو:یادکرد-ویکی