قضیه تالس (دایره)

الگو:درباره قضیه تالس در هندسه این مطلب را بیان می‌کند که اگر A و B و C نقاط روی دایره باشند و خط AC قطر دایره باشد، آن وقت زاویه ABC یک زاویهٔ قائمه خواهد بود. به بیان دیگر مرکز دایره محیطی مثلث روی یکی از اضلاع مثلث قرار می‌گیرد، اگر و تنها اگر آن مثلث قائم‌الزاویه باشد.

تاریخچه

تالس اولین کسی نبود که این قضیه را کشف کرد؛ قبل از او مصریان و بابلیان این قضیه را می‌دانستند ولی تالس آن را اثبات کرد و به نام او نیز معروف شد.

اثبات

اثبات قضیهٔ تالس

فرض کنیم $O$ مرکز دایره باشد. آنگاه $OA=OB=OC$ و $△OAB$ و $△OBC$ متساوی‌الساقین خواهند بود. در نتیجه $\widehat{BAO}=\widehat{ABO}$ و $\widehat{OCB}=\widehat{OBC}$.

با جابجایی نقطهٔ B روی محیط دایره زاویهٔ B تغییری نمی‌کند و ۹۰ درجه می‌ماند

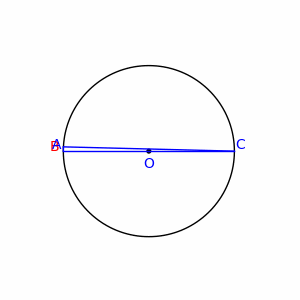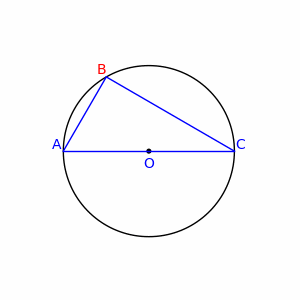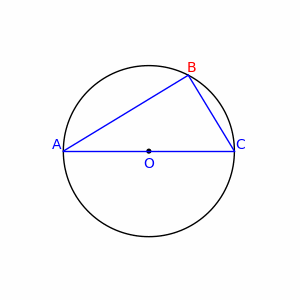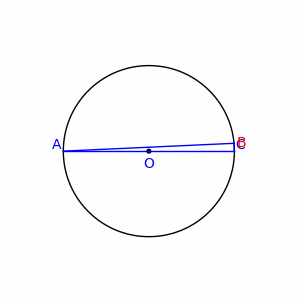
فرض کنیم $\alpha =\widehat{ABO}$ و $\beta =\widehat{OCB}$. چون جمع زوایای داخلی مثلث برابر ۱۸۰ درجه‌است پس:

$\widehat{OCB}+\widehat{ABC}+\widehat{BAO}=2\alpha +2\beta =180^{\circ }\Rightarrow \alpha +\beta =90^{\circ }$

$\widehat{ABC}=\alpha +\beta =90^{\circ }$

منابع

قضیه تالس | دانشنامهٔ رشد

پیوند به بیرون

اثبات قضیه تالس